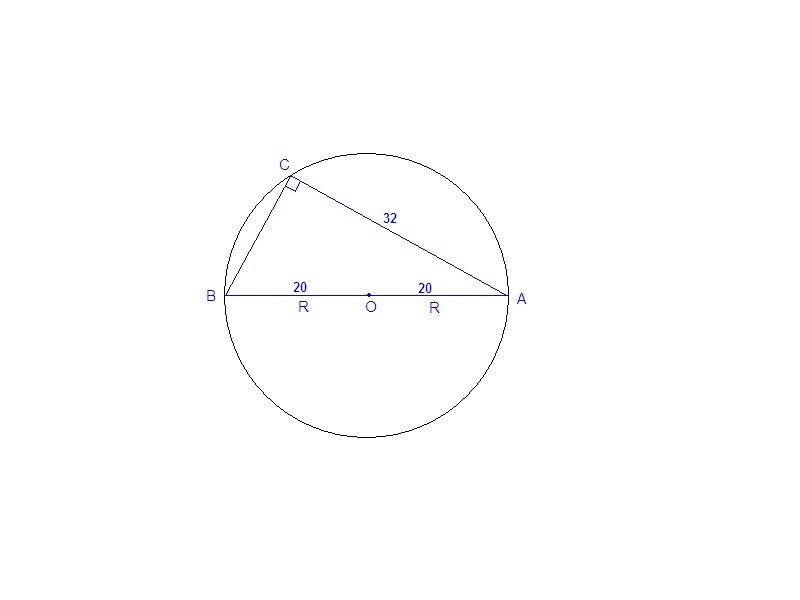
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 20. Найдите BC, если AC=32.

1 ответ

Посмотреть ответы

Megamozg

2205

Все вершины треугольника лежат на описанной окружности.
Если центр описанной окружности лежит на стороне треугольника, то эта сторона является диаметром окружности. Значит противоположный угол опирается на полуокружность, он вписанный и поэтому равен половине дуги, на которую опирается, т.е. 90°, ⇒
ΔАВС прямоугольный, АВ = 2R = 2 · 20 = 40.
По теореме Пифагора:
ВС = √(АВ² - АС²) = √(40² - 32²) = √((40 - 32)(40 + 32)) = √(8 · 72) =
= √(2 · 4 · 2 · 36) = 2 · 2 · 6 = 24

Хороший ответ

17 января 2023 04:03

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Один из углов ,образовавшихся при пересечении двух прямых, в четыре раза меньше другого. Найдите эти углы.... Помогите пожалуйста с решением .  Даны векторы  а  (3; –4) и  b  (m; 9). При каком значении m векторы  а  и&n... Диоганали четырехугольника равны 9 и 31. Найдите периметр четырехугольника ,вершинами которого являются середины сторон данного четырехугольника... Докажите что радиус окружности вписанной в прямоугольный Прямоугольный треугольник с катетами А и b гипотенузой C вычисляется по формуле r равно a+b-c... Помоогите срочно Биссектриса равностороннего треугольника равна половине стороны треугольника.Это утверждение... 1.может быть верно 2.верно всегда 3.н...