высота цилиндра равна 8 см, радиус основания 5 см, на расстоянии 4 см от оси цилиндра параллельно ей проведено сечение, найти площадь этого сечения

1 ответ

Посмотреть ответы

DevAdmin

1720

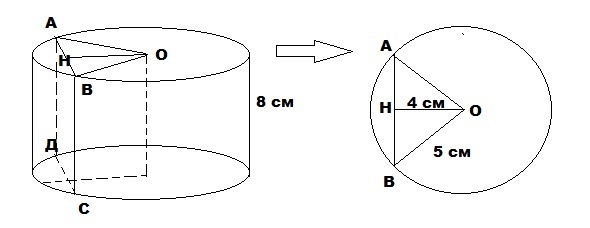
Построим цилиндр и проведем сечение (АВСД), удовлетворяющее условиям задачи.
Данное сечение является прямоугольником со сторонами равными высоте данного цилиндра (АД и ВС) и хорде, удаленной на 4 см от центра основания (Центра окружности О) (АВ и ДС).
Найдем данную хорду:
Рассмотрим треугольник АОВ где АВ хорда данной окружности, АО и ВО радиусы, а ОН высота (расстояние от центра окружности до хорды). Так как АО=ВО то высота будет являться и медианой – то есть АВ= АН*2.
По теореме Пифагора найдем АН
АН=√(АО²-ОН²)=√(5²-4²)=√9=3 см.
Значит АВ=3*2=6 см.
Площадь данного сечения равна:

Sabcd=АВ*ВС=6*8=48 кв. см.

Хороший ответ

17 января 2023 09:44

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Найти площадь фигуры. Расписать, как нашёл... Синус острого угла A треугольника ABC равен √7÷4. Найдите cos A... Сторона ромба равна 7 см, а расстояние от точки пересечения диагоналей ромба до неё равно 3см. Найдите площадь ромба. Помогите пожалуйста 8 класс... Площадь треугольника АВС равна 576 квадратных сантиметров. На стороне АС отмечена точка М так, что АМ:МС=1:2, а на стороне ВС отмечена точка Н так, чт... Чему равна длина гипотенузы прямоугольного треугольника...