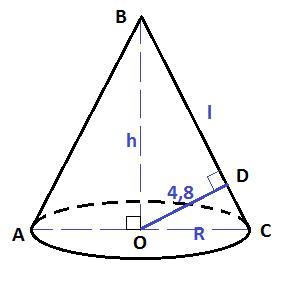
Площадь боковой поверхности конуса равна 60пи см^2. Расстояние от центра основания до образующей равна 4,8 см. Найти объем конуса.

1 ответ

Посмотреть ответы

Megamozg

2205

Дано : конус, OC = OA = R, BA = BC = $l$ - образующие,
Sбок = 60π см² , OD⊥BC, OD = 4,8 см
Найти : V
Решение :
BO = h - высота конуса, ΔВОС - прямоугольный
ΔВОС ~ ΔВDО по общему острому углу ∠OBD
$\dfrac =\dfrac\ \ \Rightarrow\ \ OC\cdot BO=OD\cdot BC\ \ \Rightarrow\ \ \boldsymbol$
Sбок = $\pi Rl=60\pi\ \ \ \Rightarrow\ \ \ \boldsymboll}$
Объём конуса
$V=\dfrac 13\cdot \pi R^2h=\dfrac {\pi}3\cdot R\cdot Rh=\dfrac {\pi}3\cdot \dfracl\cdot 4,8l=\pi\cdot 20\cdot 4,8=96\pi$
Ответ : 96π см³

Хороший ответ

17 января 2023 14:17

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Всякая ли фигура имеет центр симметрии ? Приведите пример .... Дана четырёхугольная пирамида,в основании которой лежит ромб.Все высоты боковых граней,проведённые из вершин,равны 53.Высота пирамиды равна 45.Острый... Чему равен острый угол между биссектрисами острых углов прямоугольного треугольника... О - центр окружности, описанной около ДАВС, О, - центр окружности, вписанной в ДАВС. Найти площадь АВС. АВ=ВС, АВ=17,ВС=16... Углы выпуклого четырехугольника относятся как 1:2:3:4 найдите меньший угол...