Определите угол при вершине осевого сечения конуса, если разверткой его боковой поверхности являеться сектор с дугой, равной 120 градусов.

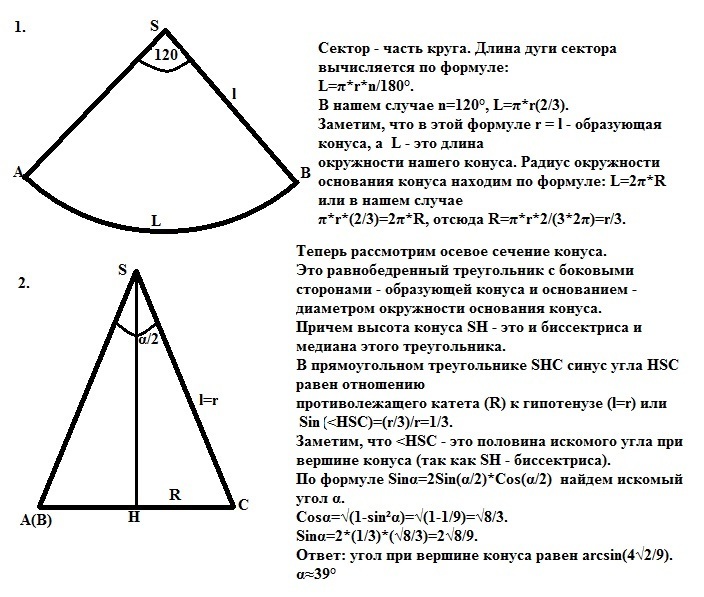
Сектор - часть круга. Длина дуги сектора вычисляется по формуле:
L=π*r*n/180°.
В нашем случае n=120°, L=π*r(2/3).
Заметим, что в этой формуле r = l - образующая конуса, а L - это длина
окружности нашего конуса. Радиус окружности основания конуса находим по формуле: L=2π*R или в нашем случае
π*r*(2/3)=2π*R, отсюда R=π*r*2/(3*2π)=r/3.
Теперь рассмотрим осевое сечение конуса.
Это равнобедренный треугольник с боковыми сторонами - образующей конуса и основанием - диаметром окружности основания конуса.
Причем высота конуса SH - это и биссектриса и медиана этого треугольника.
В прямоугольном треугольнике SHC синус угла HSC равен отношению
противолежащего катета (R) к гипотенузе (l=r) или Sin(<HSC)=(r/3)/r=1/3.
Заметим, что <HSC - это половина искомого угла при вершине конуса (так как SH - биссектриса).
По формуле Sinα=2Sin(α/2)*Cos(α/2) найдем искомый угол α.
Cosα=√(1-sin²α)=√(1-1/9)=√8/3.
Sinα=2*(1/3)*(√8/3)=2√8/9.
Ответ: угол при вершине конуса равен arcsin(4√2/9).
α≈39°

Угол при вершине осевого сечения конуса можно найти по теореме косинусов:
Cosα=(a²+b²-c²)2ab, где α - угол между сторонами a и b треугольника.
Тогда
Cosα=(2r²-(4/9)r²)/2r² = 14/18=7/9≈0,777.
α=arccos0,777 или α≈39°.