Лучшие помощники
- Megamozg 2205 б
- Matalya1 1800 б
- DevAdmin 1720 б
- arkasha_bortnikov 900 б
- Dwayne_Johnson 870 б
20 марта 2023 07:57
1264
В треугольник со сторонами 10, 14 и 16 вписан круг. Точка произвольно ставится в треугольник. Найти вероятность, что точка попадет в круг.
2
ответа
Вероятность равна соотношению площади круга и площади треугольника.
Площадь треугольника находим по формуле Герона.
Касательно окружности: находим радиус вписанной окружности, затем площадь.
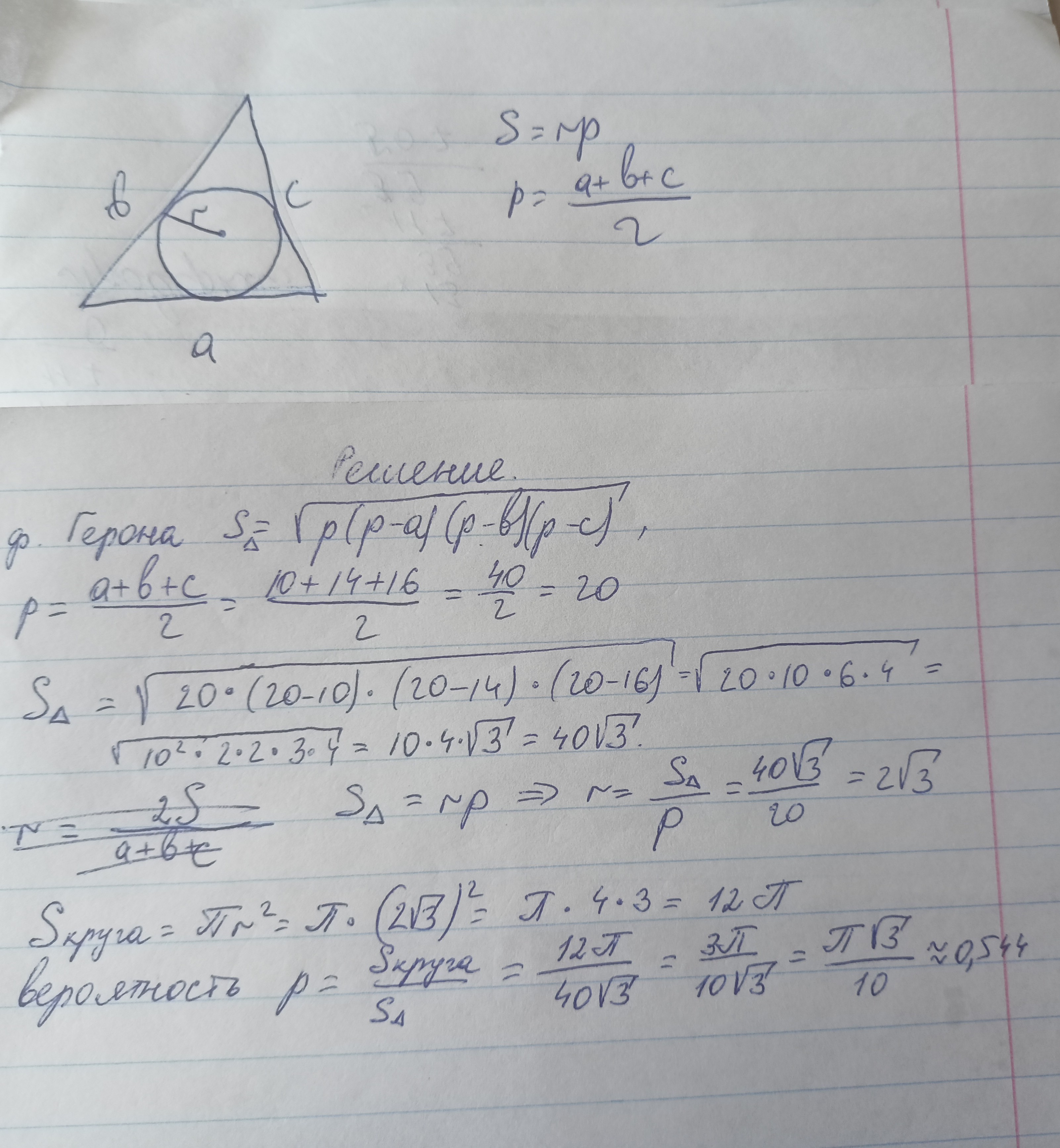
0
·
Хороший ответ
20 марта 2023 09:58
Для решения задачи воспользуемся формулой для радиуса вписанной окружности в треугольник:
$$r = \frac{2S}{a+b+c},$$
где $S$ - площадь треугольника, $a$, $b$ и $c$ - длины его сторон.
Известно, что стороны треугольника равны 10, 14 и 16. Найдем площадь треугольника по формуле Герона:
$$S = \sqrt{p(p-a)(p-b)(p-c)},$$
где $p$ - полупериметр треугольника (полусумма длин его сторон):
$$p = \frac{a+b+c}{2} = \frac{10+14+16}{2} = 20.$$
Тогда
$$S = \sqrt{20\cdot10\cdot6\cdot4} = 48.$$
Подставляя значения $S$, $a$, $b$ и $c$ в формулу для радиуса вписанной окружности, получим:
$$r = \frac{2\cdot48}{10+14+16} = \frac{24}{15} = \frac{8}{5}.$$
Теперь рассмотрим два случая:
1. Точка выбирается равномерно на всей площади треугольника.
2. Точка выбирается равномерно на границе треугольника.
В первом случае вероятность попадания точки в круг равна отношению площади круга к площади треугольника:
$$P_1 = \frac{\pi r^2}{S} = \frac{\pi\cdot(\frac{8}{5})^2}{48} = \frac{2\pi}{15}.$$
Во втором случае вероятность попадания точки в круг равна отношению длины окружности круга к периметру треугольника:
$$P_2 = \frac{2\pi r}{a+b+c} = \frac{2\pi\cdot\frac{8}{5}}{10+14+16} = \frac{8\pi}{75}.$$
Ответ: вероятность попадания точки в круг равна $\frac{2\pi}{15}$ при выборе точки равномерно на всей площади треугольника и $\frac{8\pi}{75}$ при выборе точки равномерно на границе треугольника.
$$r = \frac{2S}{a+b+c},$$
где $S$ - площадь треугольника, $a$, $b$ и $c$ - длины его сторон.
Известно, что стороны треугольника равны 10, 14 и 16. Найдем площадь треугольника по формуле Герона:
$$S = \sqrt{p(p-a)(p-b)(p-c)},$$
где $p$ - полупериметр треугольника (полусумма длин его сторон):
$$p = \frac{a+b+c}{2} = \frac{10+14+16}{2} = 20.$$
Тогда
$$S = \sqrt{20\cdot10\cdot6\cdot4} = 48.$$
Подставляя значения $S$, $a$, $b$ и $c$ в формулу для радиуса вписанной окружности, получим:
$$r = \frac{2\cdot48}{10+14+16} = \frac{24}{15} = \frac{8}{5}.$$
Теперь рассмотрим два случая:
1. Точка выбирается равномерно на всей площади треугольника.
2. Точка выбирается равномерно на границе треугольника.
В первом случае вероятность попадания точки в круг равна отношению площади круга к площади треугольника:
$$P_1 = \frac{\pi r^2}{S} = \frac{\pi\cdot(\frac{8}{5})^2}{48} = \frac{2\pi}{15}.$$
Во втором случае вероятность попадания точки в круг равна отношению длины окружности круга к периметру треугольника:
$$P_2 = \frac{2\pi r}{a+b+c} = \frac{2\pi\cdot\frac{8}{5}}{10+14+16} = \frac{8\pi}{75}.$$
Ответ: вероятность попадания точки в круг равна $\frac{2\pi}{15}$ при выборе точки равномерно на всей площади треугольника и $\frac{8\pi}{75}$ при выборе точки равномерно на границе треугольника.
0
20 марта 2023 08:00
Остались вопросы?
Еще вопросы по категории Математика
Какое количество часов эквивалентно 100 минутам?...
Ученик купил тетрадей в клетку в 3 раза больше чем тетрадей в линейку причём их было на 18 больше чем тетрадей в линейку.Сколько всего тетрадей купил...
При каких значениях k прямая y=kx+6 является касательной...
Вычислите сумму (+48)+(+25)=...
Какое число является наибольшим в данном задании?...