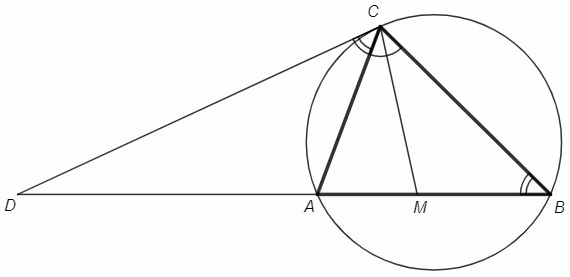
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=9 и MB=12. Касательная к описанной окружности треугольника ABC, проходящая через точку С, пересекает прямую AB в точке D. Найдите CD.

1 ответ

Посмотреть ответы

DevAdmin

1695

∠ACD =∪AC/2 =∠ABC (угол между касательной и хордой)
△ACD~△CBD (по двум углам, ∠D - общий)
AC/CB =CD/BD =AD/CD
AC/CB =AM/MB =9/12 =3/4 (по теореме о биссектрисе)
BD=4/3 CD, AD=3/4 CD
BD-AD=AB => 4/3 CD -3/4 CD =21 <=> CD=21*12/7 =36

Или
∠ACD =∪AC/2 =∠B =>
∠DCM =∠ACD+∠C/2 =∠B+∠C/2 =∠DMC
△CDM - равнобедренный, DC=DM
Квадрат касательной равен произведению секущей на ее внешнюю часть.
DC^2 =DB*DA
DA=DM-AM, DB=DM+MB
DC^2 =(DC+MB)(DC-AM) <=>
DC^2 =DC^2 +MB*DC -AM*DC -AM*MB <=>
DC=AM*MB/(MB-AM) =9*12/(12-9) =36

Хороший ответ

3 апреля 2023 19:57

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Дан параллелепипед abcda1b1c1d1 укажите компланарные 3 вектора A) ab, bc, cc1 B)aa1,ac,d1b1 C)aa1,bc,cd D)aa1,dd1,ac... Найдите sin a если. cos a =4\5... Даны компланарные векторы ~a, ~b и ~c, причем a = 3, b = 2, c = 5, ( c~a,~b) = 60◦ и ( ~cb,~c) = 60◦ . Построить вектор ~u = ~a + ~b − ~c и вычислить... Высота цилиндра 8 дм, радиус основания 5 дм. Цилиндр пересечен плоскостью так, что в сечении получился квадрат. Найдите расстояние от этого сечения до... Свойство биссектрисы треугольника...