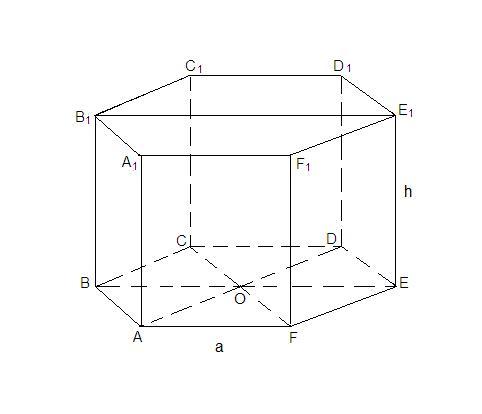
Площадь наибольшего диагонального сечения правильной шестиугольной призмы равна 10. Найдите площадь боковой поверхности этой призмы.

1 ответ

Посмотреть ответы

Megamozg

2205

Ответ:
30 кв. ед.
Объяснение:
В основании правильной призмы - правильный шестиугольник.
Радиус окружности, описанной около правильного шестиугольника, равен его стороне.
Большая диагональ его - диаметр описанной окружности.
Пусть а - сторона основания, тогда
ВЕ = 2а
BB₁E₁E - большее диагональное сечение, прямоугольник.
$S_=BE\cdot EE_1=2ah=10$
Площадь боковой поверхности:
Sбок. = Pосн. · h = 6a · h = 3 · (2ah) = 3 · 10 = 30 кв. ед.

Хороший ответ

3 апреля 2023 20:29

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

С помощью циркуля и линейки постройте биссектрису угла треугольника, и докажите что это биссектриса... Площадь ромба равна 27, а периметр равен 36. Найти высоту ромба... Боковые грани призмы ( какими фигурами являются)? Помогите пожалуйста... Основание прямой призмы-прямоугольный треугольник с катетами 6 и 8 см объем 240. найти площадь полной поверхности призмы... 7класс № 255. В равнобедренном треугольнике CDE с основанием CE проведена высота CF. Найдите угол ECF,если угол D=54градуса...