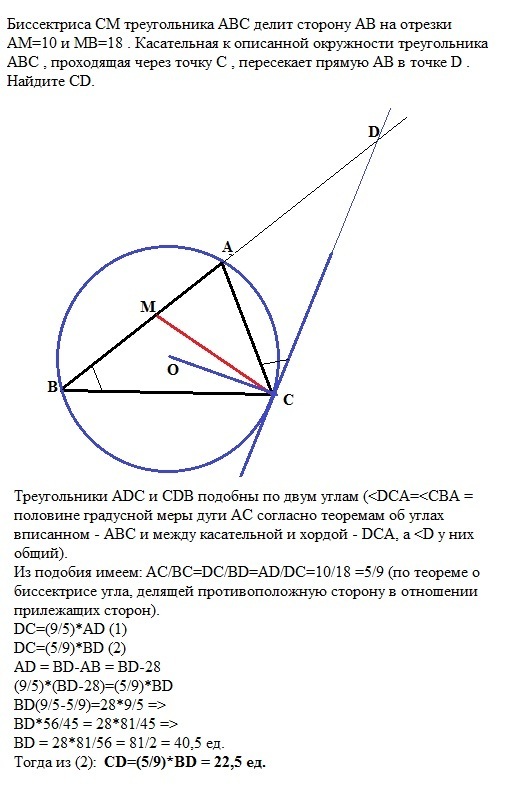
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=10 и MB=18 . Касательная к описанной окружности треугольника ABC , проходящая через точку C , пересекает прямую AB в точке D . Найдите CD .

1 ответ

Посмотреть ответы

DevAdmin

1720

Треугольники ADC и CDB подобны по двум углам (<DCА=<CВА = половине градусной меры дуги АС согласно теоремам об углах вписанном - АВС и между касательной и хордой - DCA, а <D у них общий).
Из подобия имеем: АС/ВС=DC/BD=AD/DC=10/18 =5/9 (по теореме о биссектрисе угла, делящей противоположную сторону в отношении прилежащих сторон - АС/ВС=АМ/МВ).
Тогда из этих соотношений:
DC=(9/5)*AD (1)
DC=(5/9)*BD (2).
АВ=28 (дано), AD = BD-AB = ВD-28.
Приравняем (1) и (2):
(9/5)*(ВD-28)=(5/9)*BD
BD(9/5-5/9)=28*9/5 =>
BD*56/45 = 28*81/45 =>
BD = 28*81/56 = 81/2 = 40,5 ед.
Тогда из (2): СD=(5/9)*BD = 22,5 ед.

Хороший ответ

3 апреля 2023 21:11

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Дано: AB перпендикулярно плоскости альфа. Наклонная AC=8. Её проекция=7. наклонная AD=4. Найти проекцию AD на плоскость альфа.... Медиана прямоугольного треугольника, проведённая к гипотенузе , разбивает его на треугольника с периметрами 8 и 9. Найти стороны треугольника.... Докажите, что уравнение является уравнением сферы. x^2 - 4x + y^2 + z^2 = 0 объясните.... SABCD - правильная пирамида, SM и SK - апофемы, S(ABCD)=2S(KSM), площадь боковой поверхности равна 16√5. Найти S(ABCD).... Площадь вписанного в окружность треугольника ,описанного около окружности треугольника...