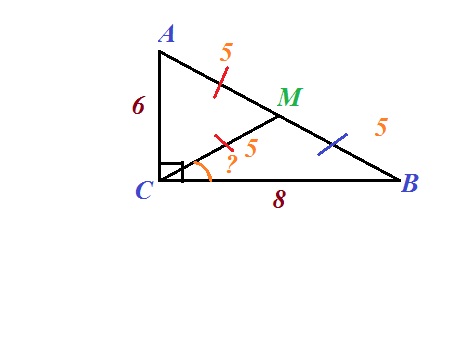
в прямоугольном треугольнике с катетами 6 и 8 проведена медиана к гипотенузе. Найдите синус угла между большим катетом и медианой.

2 ответа

Посмотреть ответы

Megamozg

2205

Медиана,проведённая из вершины прямого угла прямоугольного треугольника равна половине гипотенузы(по свойству прямоугольного треугольника).Пусть угол АСВ в прямоуг.треуг.-прямой,АВ-гипотенуза,СМ- медиана,АВ= корень квадратный из(8^2+6^2)=10(по теореме Пифагора).СМ=10/2=5.ВМ=1/2АВ=5,т.к. СМ медиана.Т.к. СМ=ВМ,то треугольник ВМС-равнобедрынный,тогда в нём угол МВС равен углу ВСМ,следовательно синус угла ВСМ(искомый)=синусу угла ВМС = АС/АВ=6/10=0,6.Ответ:0,6

Хороший ответ

3 апреля 2023 22:01

DevAdmin

1720

Чертеж во вложении.
Найдем гипотенузу АВ в треугольнике АВС по теореме Пифагора:
$AB^2=AC^2+BC^2$
$AB=\sqrt=\sqrt=\sqrt=10$
Медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы. Поэтому МС=МА=МВ=5.
медиана треугольника делит его на два треугольника с равными площадями.
$S_=\frac=\frac=24$
Значит площади АСМ и СМВ равны по 12.
$S_=\fracCM*CB*sin MCB$
$\fracCM*CB*sin MCB=12$
$5*8*sin MCB=24$
$sin MCB=\frac=\frac=0,6$
Ответ: 0,6

3 апреля 2023 22:01

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Записать уравнение прямой, проходящей через точки А(-2;-1) и В(3;1)... Углы DEF и MEF - смежные, луч EK - биссектриса угла DEF, угол KEF в 4 раза меньше уг- ла MEF. Найдите углы DEF и MEF.... определить знак выражения. cos 40° sin 70° cos 113° sin 240° cos 290° tg 98° ctg 200° sin (-140°) cos (-300°) tg (-120°)... дана правильная четырехугольная призма abcda1b1c1.найдите площадь сечения проходящего через ребро ac и вершину b1 если сторона основания призмы равна... 1)сформулируйте и докажите теорему о разложении вектора по двум не коллинеАрным векторам . 2)объясните,как вводится прямоугольная система координат....