Площадь параллелограмма ABCD равна 115. Точка Е - середина стороны AD. Найдите площадь треугольника ABE

1 ответ

Посмотреть ответы

Megamozg

2205

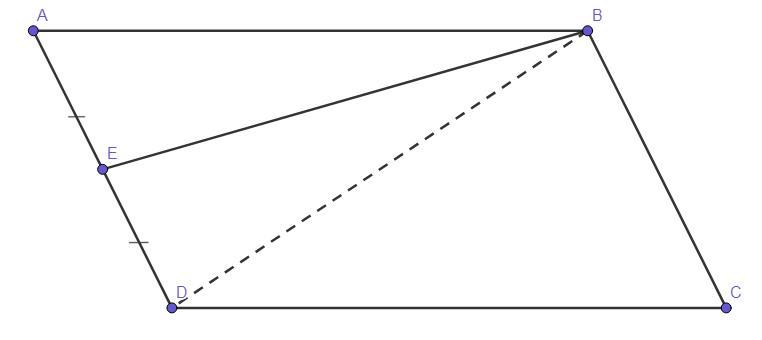
Чертёж смотрите во вложении.

Дано:

Четырёхугольник АBCD - параллелограмм.
S(АBCD) = 115 (ед²).
Точка Е - середина AD.

Найти:

S(ΔАВЕ) = ?

Решение:

Проведём диагональ BD. По свойству параллелограмма имеем, что - ΔABD = ΔCDB. У равных многоугольников равные площади. Следовательно, S(ΔABD) = 0,5*S(АBCD).
Рассмотрим ΔАВЕ. Отрезок ЕВ - медиана ΔАВЕ, так как соединяет серединную точку Е стороны AD с вершиной треугольника В.
Медиана треугольника делит треугольник на два равновеликих треугольника. То есть, S(ΔАВЕ) = 0,5*S(ΔABD) ⇒ S(ΔАВЕ) = 0,5*0,5*S(АBCD) ⇒ S(ΔАВЕ) = 0,25*S(АBCD).
S(ΔАВЕ) = 0,25*115 (ед²)
S(ΔАВЕ) = 28,75 (ед²).

Ответ: 28,75 (ед²).

Хороший ответ

3 апреля 2023 23:50

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

в треугольнике MNK О-точка пересечения медиан , вектор MN равен вектору x , вектор MK равен вектору y вектор MO=k ( x+y ) нийти число k... Катеты прямоугольного треугольника равны 18 и 24.Найдите высоту,проведенную к гипотенузе.... Используя данные, приведённые на рисунках, укажите номера рисунков, на которых изображены равнобедренные треугольники: 1)35 и 35 градусов у двух углов... В треугольнике ABC известно,что AB=BC, угол ABC=106 градусов .Найдите угол BCA .Ответ дайте в градусах... Даны стороны треугольников PQR и ABC: PQ= 16 см, QR=20 см, PR=28 см и АВ =12 см , ВС=15 см , АС=21 см .Найдите отношение площадей этих треугольников ....