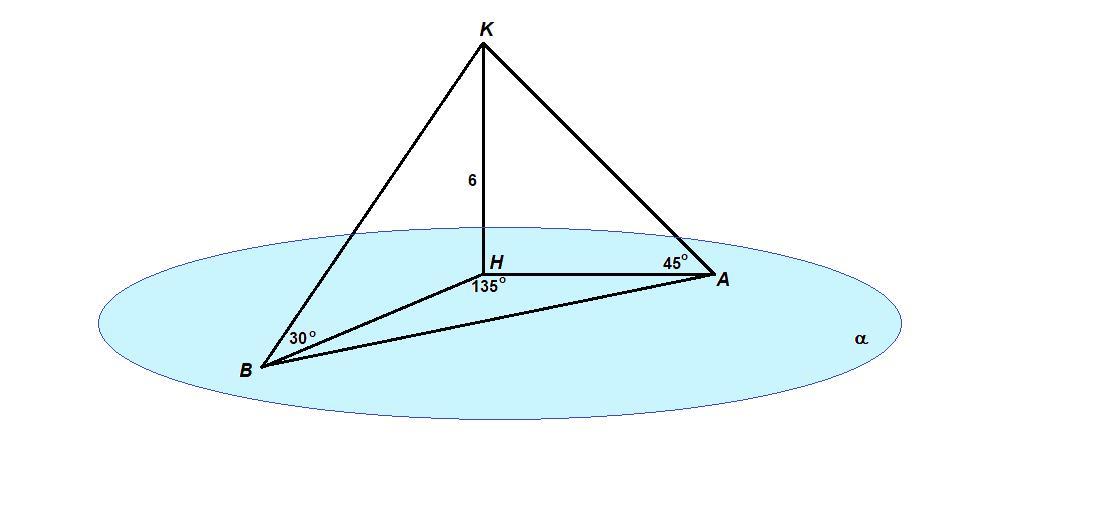
Точка К находится на расстоянии 6см. от плоскости,наклонные КА и КВ образуют с плоскостью углы 45 и 30 градусов, угол между проекциями наклонных 135 градусов. Найти неизвестные стороны.

1 ответ

Посмотреть ответы

Megamozg

2205

Ответ:
HA = 6 см
КА = 6√2 см
КВ = 12 см
НВ = 6√3 см
$AB=\sqrt}$ см

Объяснение:
Проведем KH⊥α. Тогда КН = 6 см - расстояние от точки К до плоскости α.
Угол между прямой и плоскостью - это угол между прямой и ее проекцией на эту плоскость.
НА - проекция КА на плоскость α, значит ∠КАН = 45°,
НВ - проекция КВ на плоскость α, значит ∠КВН = 30°.
∠АНВ = 135°.
ΔКНА: ∠КНА = 90°, ∠КАН = 45°, значит треугольник равнобедренный,
НА = КН = 6 см
КА = 6√2 см как гипотенуза равнобедренного прямоугольного треугольника.
ΔКНВ: ∠КНВ = 90°,
КВ = 2КН = 12 см по свойству катета, лежащего против угла в 30°,
по теореме Пифагора:
НВ = √(КВ² - КН²) = √(144 - 36) = √108 = 6√3 см
Из ΔАНВ по теореме косинусов:
АВ² = НА² + НВ² - 2·НА·НВ·cos∠AHB
cos135° = cos(180° - 45°) = - cos45° = √2/2
AB² = 36 + 108 + 2 · 6 · 6√3 · √2/2 = 144 + 36√6
$AB=\sqrt}$ см

Хороший ответ

4 апреля 2023 01:30

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

В треугольнике АВС АС=ВС=10 , АВ=16. Найдите tg угла А... Дана правильная треугольная призма ABCA1B1C1, AB = 12, AA1= 4√6. Точка K делит ребро A1B1 в отношении 1:2, считая от точки A1. Найдите площадь сечения... Найдите скалярное произведение вектора а умножить на вектор б,если модуль а=3,модуль б=4,угол(вектор а;вектор б)=120 градусов... Известно, что в прямоугольном параллелепипеде ABCDA1B1C1D1 длины отрезков AB, BC и DD1 соответственно равны 9 см, 12 см и 8 см. Точка N... Как выглядит "4 корня из 2 в квадрате" извините за тупость просто я в 6 классе, а это вроде 7-8 класс...