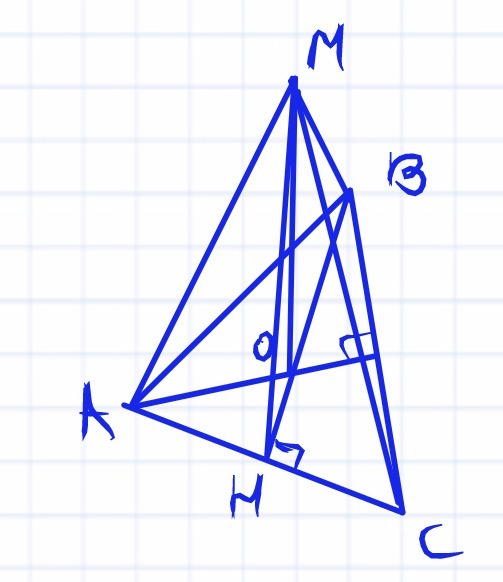
в правильном треугольнике abc точка o центр om перпендикуляр к плоскости abc найдите расстояние от точки m до стороны ab если ab=10см om=5см

1 ответ

Посмотреть ответы

Megamozg

2205

Так как точка О центр ΔАВС, ОН - радиус вписанной окружности.
$r= \frac = \frac{ \frac*AB*AC*sinBAC }{ \frac*(AB+BC+AC) }= \frac{ AB^2*sin60^o }=\frac} }=\\= \frac{ \sqrt }*AB= \frac{ \sqrt }*10=\frac }$ .
По теореме о трёх перпендикулярах МН⊥АС (МН - наклонная, ОН - проекция) ⇒ МН - искомое расстояние. Из ΔМОН, по теореме Пифагора
$MH= \sqrt= \sqrt })^2}= \sqrt}=\\=5 \sqrt{ \frac }= \frac{ \sqrt } =\frac }.$ .
Ответ: $\frac }$ см

Хороший ответ

4 апреля 2023 01:34

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Даны точки А(0;1),В(3;2),С(-2;1) и D(1;-2). а) Существует ли параллельный перенос, при котором точка А переходит в точку В, а точка С в точку D? б)... Величина одного из прилежащих к основанию углов равнобедренного треугольника 20 градусов. Определи величины угла вершины этого треугольника... вершины прямоугольника лежат на сфере радиуса 10 см. Найдите расстояние от центра сферы до плоскости прямоугольника, если диагональ равна 16 см... и последняя задача на сегодня :площадь сечения куба плоскостью,проходящей через концы трех ребер ,выходящих из одной вершины,равна 18*корень 3.Просят... Используя рисунок, укажите верные утверждения 1) угол AKD И BKD - смежные углы. 2) угол BKD И BKE - вертикальные углы 3) угол AKE - тупой угол 4) у...