Лучшие помощники
- Megamozg 2205 б
- Matalya1 1800 б
- DevAdmin 1720 б
- arkasha_bortnikov 900 б
- Dwayne_Johnson 870 б
2 апреля 2023 02:34
987
Даю 80 баллов!(есть теория и примеры) Провести полное исследование функции и построить график : y=ln(x^2 +1)

1
ответ
Ответ:
Пошаговое объяснение:
y = ln(x² + 1)
1) x² + 1 > 0
x ∈ R
D(y) = (-∞; +∞)
2) функция непрерывна на всей числовой оси
3) y(-x) = ln((-x)² + 1) = ln(x² + 1) = y(x) - функция четная => график симметричен относительно оси Oy
функция непериодичная
4) k = lim(x->∞) f(x)/x = lim(x->∞) ln(x²+1)/x = lim(x->∞) 2x/(x³+x) = lim(x->∞) 2/(x²+1) = 0
b = lim(x->∞)(f(x) - kx) = lim(x->∞) ln(x² + 1) = ∞
график не имеет асимптот
5) y' = 2x/(x²+1) = 0 => x = 0
__(-∞; 0) | _0 _ | (0; +∞)
y' __-___|_0__|__+__
y __\/__| __0_|__/\__
0 - минимум
6) y'' = (2(x²+1) - 4x²)/(x²+1)² = (2-2x²)/(x²+1)² = 0 => x = +-1
__(-∞; -1) U (-1; 1) U (1; +∞)
y''__-______+______-___
y__∩_______U_____∩___
7) x = 0 => y = 0
y = 0 => x = 0
8) в приложении
Пошаговое объяснение:
y = ln(x² + 1)
1) x² + 1 > 0
x ∈ R
D(y) = (-∞; +∞)
2) функция непрерывна на всей числовой оси
3) y(-x) = ln((-x)² + 1) = ln(x² + 1) = y(x) - функция четная => график симметричен относительно оси Oy
функция непериодичная
4) k = lim(x->∞) f(x)/x = lim(x->∞) ln(x²+1)/x = lim(x->∞) 2x/(x³+x) = lim(x->∞) 2/(x²+1) = 0
b = lim(x->∞)(f(x) - kx) = lim(x->∞) ln(x² + 1) = ∞
график не имеет асимптот
5) y' = 2x/(x²+1) = 0 => x = 0
__(-∞; 0) | _0 _ | (0; +∞)
y' __-___|_0__|__+__
y __\/__| __0_|__/\__
0 - минимум
6) y'' = (2(x²+1) - 4x²)/(x²+1)² = (2-2x²)/(x²+1)² = 0 => x = +-1
__(-∞; -1) U (-1; 1) U (1; +∞)
y''__-______+______-___
y__∩_______U_____∩___
7) x = 0 => y = 0
y = 0 => x = 0
8) в приложении
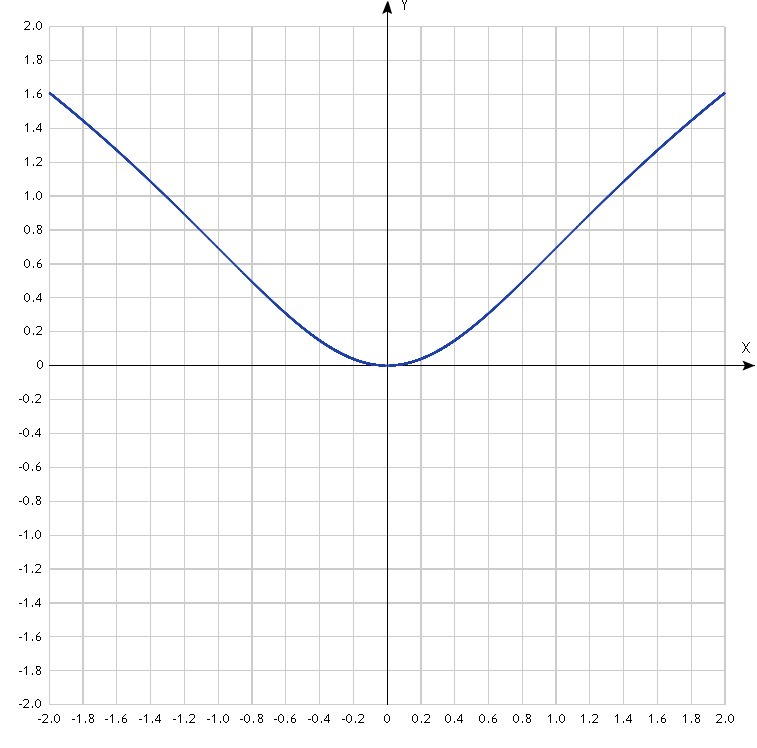
0
·
Хороший ответ
4 апреля 2023 02:34
Остались вопросы?
Еще вопросы по категории Математика
На поле, площадь которого 620 га, работали хлопкоуборочные машины. За сутки они убрали 15% всего поля. Сколько гектаров хлопка они не убрали за сутки?...
составьте уравнение прямой, проходящей через точки D (-3:9) и K (5;-7)...
Как изменится значение выражения 1 cos 2 a, если угол a увеличить на pi/4 (45 градусов)?...
Сократите, а затем приведите к наименьшему общему знаменателю дроби: a)75/90; 44/99; 33/44; б)40/64; 42/144; 100/180....
На основании имеющихся данных о режиме работы и эффективности использования РВ в ОАО «Мастер» проанализируйте использование фонда рабочего времени спо...