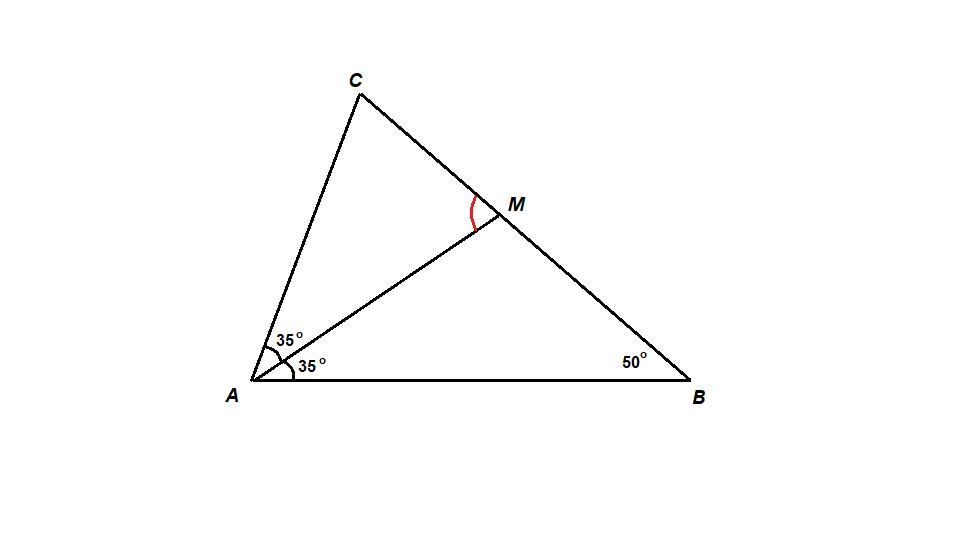
В треугольнике ABC известно , что ∠A=70° , ∠B=50°. Биссектриса ∠A пересекает сторону BC в точке M . Найдите угол AMC.

1 ответ

Посмотреть ответы

Megamozg

2205

Ответ:
85°
Объяснение:
Сумма углов треугольника равна 180°, значит
∠С = 180° - (∠А + ∠В) = 180° - (70° + 50°) = 180° - 120° = 60°
∠САМ = 1/2 ∠А = 1/2 · 70° = 35°, так как АМ биссектриса.
Из ΔАСМ:
∠АМС = 180° - (∠САМ + ∠АСМ) = 180° - (35° + 60°) = 180° - 95° = 85°

Хороший ответ

4 апреля 2023 04:35

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Какие виды параллелограмма бывают?... В равнобедренном треугольнике ABC проведена высота BD к основанию AC. Длина высоты — 10,8 см, длина боковой стороны — 21,6 см. Определи углы этого тр... Найдите радиус шара описанного около правильной треугольной пирамиды, в которой боковое ребро составляет угол 30 градусов с плоскостью основания, а дл... Сколько градусов острый угол?... Решите пожалуйста! В треугольнике 2 угла равны 43 и 88 градусов. Найдите его 3 угол...