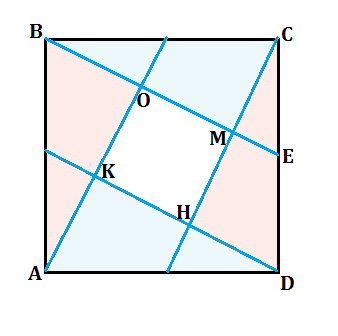
В квадрате каждая вершина соединена с серединой стороны, которая лежит между двумя следующими вершинами (считать вершины в одинаковом порядке). Соединенные прямые образуют своим пересечением квадрат. Доказать, что его площадь составляет 1/5 площади данного квадрата.

Ну вот если продлить отрезки, соединяющие вершины с серединами сторон, а из вершин провести прямые параллельно этим отрезкам, то при пересечении они образуют
1) попарно равные треугольники с треугольниками, образовались которые внутри квадрата
2) четыре квадрата, равных квадрату, образованному внутри (площадь которого надо найти). Это проще всего понять, если заметить, что вся эта конструкция переходит в себя при повороте на 90° вокруг центре исходного квадрата - поскольку "в себя" переходят и вершины, и середины сторон.
Кстати, это доказывает и то, что фигура, площадь которой надо найти - тоже квадрат. В условии это сказано, но не ясно, откуда это следует.
Поскольку все таких квадратов 5, и все они одинаковые, и площадь их (из за пункта 1) равна площади исходного квадрата, все доказано.

Вариант решения.
Несложно заметить, что образовавшийся квадрат в центре исходного окружен равными прямоугольными треугольниками. У них углы при вершинах квадрата ОМНК прямые и равны гипотенузы - стороны исходного квадрата.
Δ АОВ= Δ ВМС=Δ СНД=Δ ДКА
Искомая площадь равна площади исходного квадрата без суммы площадей этих треугольников или без учетверенной площади треугольника ВМС
Рассмотрим треугольники ВСЕ и ВМС.
Они подобны - прямоугольные с общим острым углом при В.
Пусть сторона квадрата равна а.
Тогда СЕ=а/2
По т. Пифагора ВЕ=√(ВС²+СЕ²)=(а√5):2
ВМ:ВС=ВС:ВЕ
ВМ=ВС²:ВЕ=2а/√5
Δ ВСЕ~Δ СМЕ - прямоугольные с общим острым углом при Е.
ВС:СМ+ВМ:СЕ
ВС*СЕ=СМ*ВМ
а*а/2=СМ*(а√5)2 ⇒
CМ=а/√5
Площадь Δ ВСМ=ВМ*СМ:2
S (ВСМ)=(2а/√5)*(а/√5):2=а²/5
S ☐ ABCD=a²
S☐КОМН=а² - 4*а²/5=а²/5, т.е. 1/5 площади данного квадрата.