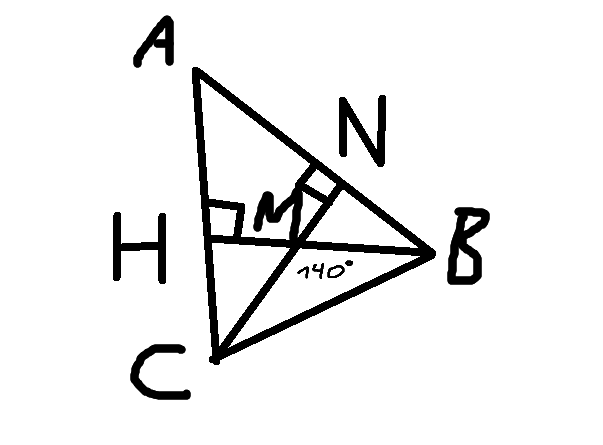
Высоты, проведенные к боковым сторонам АВ и АС остроугольного равнобедренного треугольника АВС, пересекаются в точке М. Найдите углы треугольника, если угол BMC=140

1 ответ

Посмотреть ответы

Megamozg

2205

Т.к. <CMN и <HMB - развернутые, то они равны по 180 градусов, тогда <HMC=<NMB=180-140=40 градусов каждый.Т.к. BH и CN - высоты, то <CHM и <MNB равны по 90 градусов каждый. Т.к. сумма градусных мер углов любого треугольника равна 180 градусам, то <HCM=<MBN=180-40-90=50 градусов каждый. Рассмотрим треугольники ANC и HAB, т.к. угол <CAB - общий, CA=AB(т.к. ABC - равнобедренный), <HCM=<MBN=50, то они равны, значит высоты BH и CN равны и AH=AN, тогда если AB=AC и AH=AN, то CH=NB. Если <CNB=<CHB, CN=BH, CH=NB, то треугольники CHB и CNB равны, тогда <HCB=<CBN. Т.к. <HCM=<MBN=50 и <HCB=<CBN, то <MCB=<MBC. Т,к. сумма градусных мер углов любого треугольника равна 180 градусам, то <MCB+<MBC=180-140=40 градусов, а т.к. <MCB=<MBC, то они оба равны по 40:2=20 градусов, значит <ACB=<CBA(т.к. ABC - равнобедренный)=50+20=70 градусов каждый, тогда если сумма градусных мер углов любого треугольника равна 180 градусам, то <CAB=180-70-70=40 градусов.
Ответ: <ACB=<ABC=70 градусов и <CAB=40 градусов.

Хороший ответ

4 апреля 2023 08:25

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

диагонали прямоугольника abcd пересекаются в точке o. Перпендикуляр АМ ,опущенный на диагональ BD , разбивает отрезок OB на части : OM =12см и BM = 3... В остроугольном треугольнике АВС проведены высоты АК и СЕ = 12см,ВЕ=9см,АК=10см.Найдите площадь треугольника АВС.... В точке В проведена касательная к окружности с центром О, проведен радиус в точку касания. Найдите угол АОВ, если угол АОВ=35°(смотри рисунок)... ПОмогите! Две стороны треугольника равны B и C, а биссектриса угла между ними равна l. Найти третью сторону треугольника и найти значение если b=1,c=4... Найдите периметр участка земли прямоугольной формы, если площадь участка равна 3600 м2, а одна сторона в 4 раза больше другой. Ответ дайте в метрах. Р...