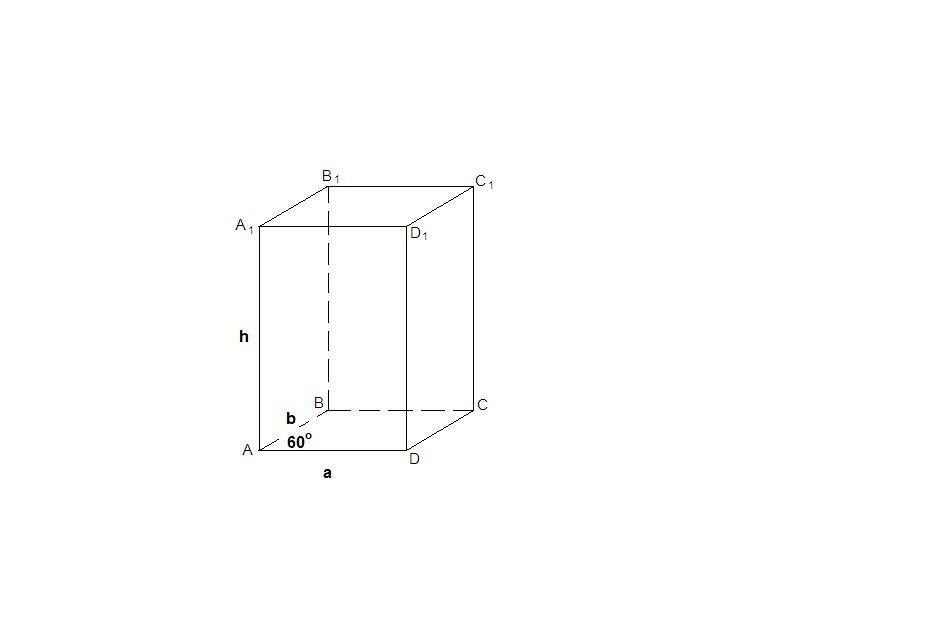
в прямом параллелепипеде стороны основания равны 3 см и 4 см, а угол между ними-60. Площадь боковой поверхности ровна 15√3 см². Найти объём параллелепипеда.

1 ответ

Посмотреть ответы

Megamozg

2205

Ответ: 135/7 см³

Объяснение:
Площадь боковой поверхности прямого параллелепипеда:
Sбок = Pосн · h
Pосн = (a + b) · 2 = (3 + 4) · 2 = 14 см
h = Sбок / Pосн = 15√3/14 см
Основание параллелограмм, его площадь:
Sосн = ab · sin60° = 3 · 4 · √3/2 = 6√3 см²
Объем:
V = Sосн · h = 6√3 · 15√3/14 = 135/7 см³

Хороший ответ

4 апреля 2023 09:54

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

1)Через точку А окружности проведены диаметр АС и две хорды АВ и АD , равные радиусу этой окружности . Найдите углы четырехугольника АВСD и градусные... Что такое абсолютная величина вектора?... Углы, отмеченные на рисунке одной дугой, равны. Найдите угол α . Ответ дайте в градусах.... ребро куба ABCDA1B1C1D1 равно a точка P- середина ребра D1C1. Найдите расстояние до плоскости BPD от точек: а) A1, ) A, и) C1... Отрезок АЕ перпендикулярен к плоскости равностороннего треугольника АВС. Стороны треугольника 6см, АЕ = 3см. Найдите расстояние от концов отрезка АЕ...