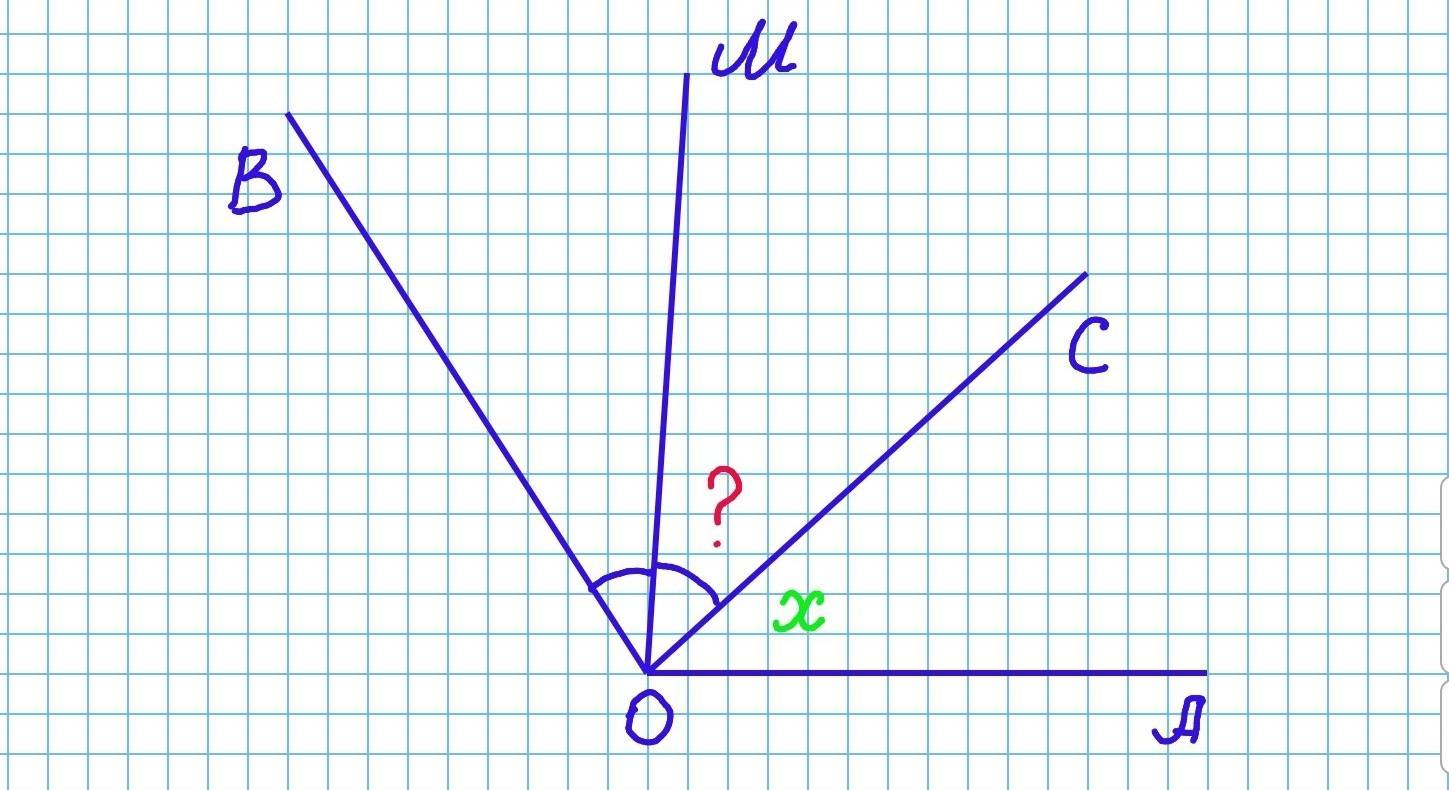
Между сторонами угла АОВ, равного 140°, проведены лучи ОС и ом так, что угол АОСна 16° меньше угла ВОС, а OM — биссектриса угла Вос. Найдите величину угла COM.
Ответ дайте в градусах.
Запишите решение и ответ.

1 ответ

Посмотреть ответы

DevAdmin

1720

Ответ:
∠СОМ=39°
Объяснение:
Дано: ∠AOВ=140°, ОМ - биссектриса
Найти: ∠СОМ
Пусть угол АОС равен х градусов, тогда угол ВОС равен х+16°. Так как сумма этих углов равна углу АОВ, составляем уравнение:
∠АОС+∠ВОС=∠AOВ
х+х+16=140
2х=140-16
2х=124
х=62

∠АОС=62°, ∠ВОС=62°+16°=78°.

Так как ОМ - биссектриса ∠ВОС, то по свойству биссектрисы:
∠СОМ=½•∠ВОС=½•78°=39°.

Величина угла СОМ равна 39°.

Хороший ответ

4 апреля 2023 10:52

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Чему равен вписанный угол, который опирается на дугу, градусная мера которой равна 317°?... В треугольнике ABC на сторонах AB и BC отмечены точки M и K соответственно так, что BM : AB = 1:2 ,а BK : BC= 4: 5. Во сколько раз площадь треугольник... Какой вектор называется разностью двух векторов?Постройте разность двух данных векторов... Вершины треугольника ABC лежат на сфере радиуса 13 см. Найдите расстояние от центра сферы до плоскости треугольника, если АВ = 6 см, ВС = 8 см, АС= 10... В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстоя...