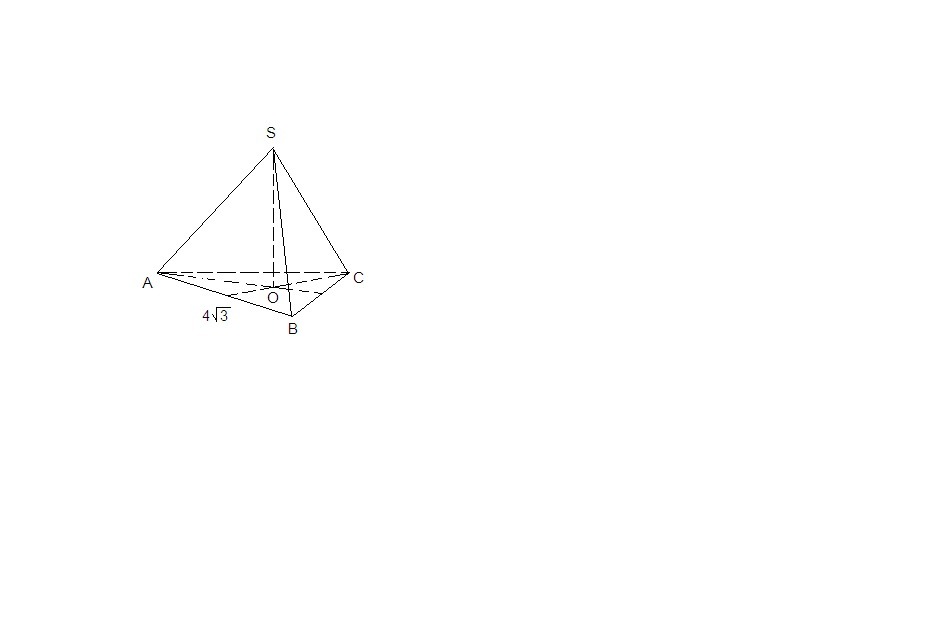
В правильной треугольной пирамиде сторона основания равна 4 корня из 3 см, а плоский угол при вершине пирамиды равен 90 градусов. Найдите высоту пирамиды.

1 ответ

Посмотреть ответы

Megamozg

2205

∠ASB = ∠ASC = ∠BSC = 90° - плоские углы при вершине пирамиды.
Пусть а - боковое ребро.
Из ΔASB по теореме Пифагора:
АВ² = SA² + SB²
48 = a² + a²
a² = 24
a = 2√6 см

АО = АВ√3/3 = 4√3 · √3 /3 = 4 см - как радиус окружности, описанной около правильного треугольника.

ΔASO: по теореме Пифагора
SO = √(SA² - AO²) = √(24 - 16) = √8 = 2√2 см

Хороший ответ

4 апреля 2023 10:54

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

В равнобедренном треугольнике MPK стороны MP и PK равны, угол К=40 градусов, MK=9 см. Из вершины P проведена биссектриса PH. Постройте чертёж. Найдите... Срочно!!!! Дана трапеция ABCD (AD||BC), диагонали трапеции пересекаются в точке О, SBOC=4см^2, SCOD=8см^2. Найдите площади трапеции.... Что такое гомотетия, центр гомотетии и коэффициент... Дано векторы a и b.Построить вектор: 1)2a+b. 2) 1/3a+b 3) a-1/2b 4)-1/3a-2/3b. (/-это дроби)... на окружности с центром О отмечены точки А и В так, что угол АОВ=18.длина меньшей дуги АВ =5.Найдите длину большей дуги...