В треугольнике мнк о - точка пересечения медиан .выразите вектор мо через вектор мн=х ,мх=у

Ответ:
Вектор МО = (x+y)/3.
Объяснение:
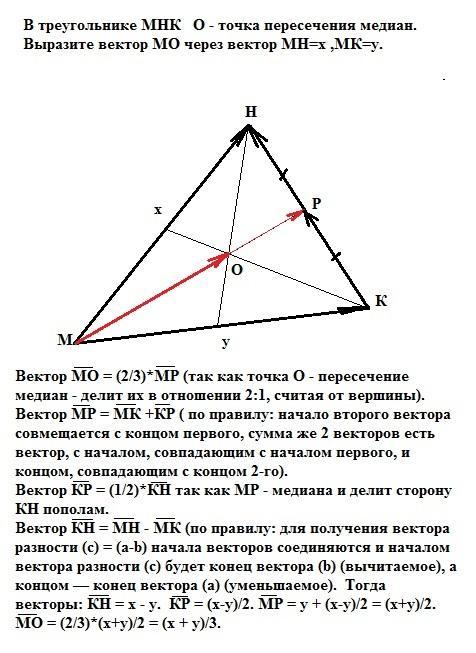
В треугольнике МНК О - точка пересечения медиан.
Выразите вектор МО через векторы МН=х, МК=у.
Решение.
Вектор МО = (2/3)*МР (так как точка О - пересечение медиан - делит их в отношении 2:1, считая от вершины).
Вектор МР = МК +КР ( по правилу: начало второго вектора совмещается с концом первого, сумма же 2 векторов есть вектор, с началом, совпадающим с началом первого, и концом, совпадающим с концом 2-го).
Вектор КР = (1/2)*КН так как МР - медиана и делит сторону КН пополам.
Вектор КН = МН - МК (по правилу: для получения вектора разности (c) = (a-b) начала векторов соединяются и началом вектора разности (c) будет конец вектора (b) (вычитаемое), а концом - конец вектора (a) (уменьшаемое). Тогда
векторы: КН = x - y. КР = (x-y)/2. MP = y + (x-y)/2 = (x+y)/2.
MO = (2/3)*(x+y)/2 = (x + y)/3.