существует ли выпуклый пятиугольник углы которого равны 100°, 110°, 155°, 165°, 200° ответ обоснуйте.

1 ответ

Посмотреть ответы

Megamozg

2205

Ответ:
Не существует!
Объяснение:
По теореме сумма пятиугольник углов любого выпуклого пятиугольника равна 540° (180°(5 - 2)).
Сложим все углы: 100° + 110° + 155°+ 165°+ 200° = 730°. Так как сумма углов больше 540° (730° > 540°), пятиугольник не является выпуклым.
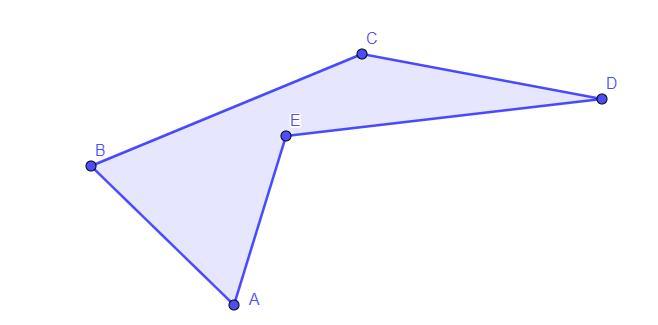
(на рисунке изображен невыпуклый многоугольник)

Хороший ответ

4 апреля 2023 10:58

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

помогите, срочно... 3. Пусть и В - углы треугольника. Известно, что 36° S a S 55°, 101° < B < 102°. Оцените величину третьего угла.... Периметр равнобедренного треугольника равен 216 , а боковые стороны равны78 . Найдите площадь треугольника.... В остроугольном треугольнике ABC высота AH равна 20√3 , а сторона AB равна 40 . Найдите cos∠B . Пожалуйста помогите)))!!... Диагонали параллелограмма равны 12 и 17, а угол между ними равен 30°. Найдите площадь этого параллелограмма. Дано и решение Ответ должен быть 51...

существует ли выпуклый пятиугольник углы которого равны 100°, 110°, 155°, 165°, 200° ответ обоснуйте.​

существует ли выпуклый пятиугольник углы которого равны 100°, 110°, 155°, 165°, 200° ответ обоснуйте.