и последняя задача на сегодня :площадь сечения куба плоскостью,проходящей через концы трех ребер ,выходящих из одной вершины,равна 18*корень 3.Просят найти ДЛИНУ РЕБРА КУБА

1 ответ

Посмотреть ответы

DevAdmin

1720

Ответ:
Ребро куба равно 6 ед.
Объяснение:
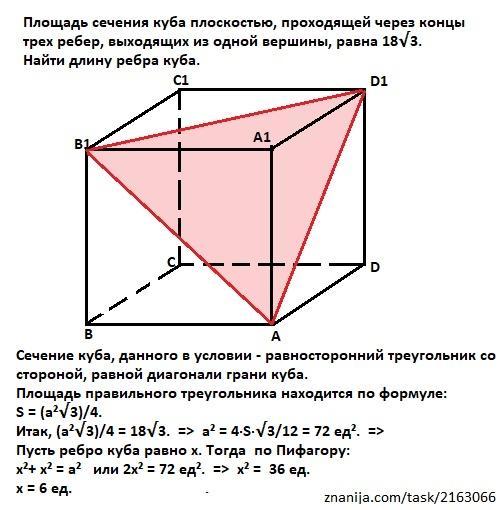
Сечение куба, данного в условии - равносторонний треугольник со стороной, равной диагонали грани куба.
Площадь правильного треугольника находится по формуле:
S = (a²√3)/4.
Итак, (a²√3)/4 = 18√3. => a² = 4·S·√3/12 = 72 ед². =>
Пусть ребро куба равно х. Тогда по Пифагору:
х²+ х² = а² или 2х² = 72 ед². => х² = 36 ед.
x = 6 ед.

Хороший ответ

4 апреля 2023 16:05

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Рассмотрим различные прямоугольники периметра 10 10, лежащие внутри квадрата со стороной 10 10. Чему равна наибольшая возможная площадь з... концы отрезка, длина которого равна 25 см, принадлежат двум перпендикулярным плоскостям, а расстояния от концов отрезка до линии пересечения плоскосте... Найти внешний угол... Дан прямоугольный треугольник АВС (угол С=90°) Точка Е принадлежит прямой АС, точка F прямой АВ, EF||CB, ЕК - биссектриса треугольника AEF. Чему равен... катет прямоугольного треугольника равен 30 см а его проекция на гепотенузу 18 см найдите гипотенузу и второй катет треугольника...