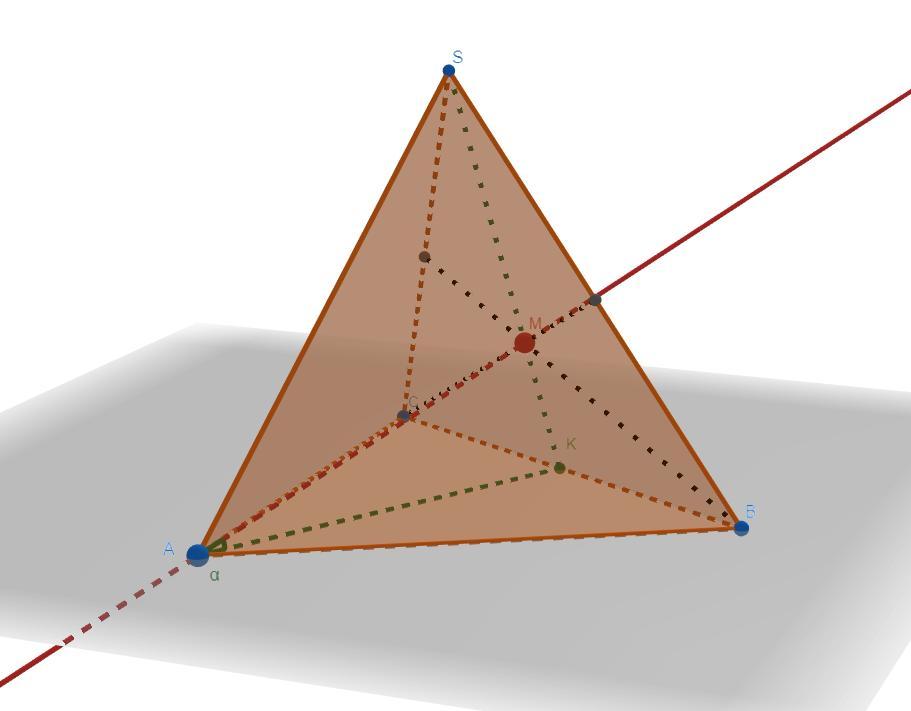
В правильной треугольной пирамиде SABC с основанием ABC известны ребра: AB=8√3, SC=17.Найдите угол, образованный плоскостью основания и прямой AM, где M - точка пересечения медиан грани SBC/
(пожалуйста, с рисунком)

1 ответ

Посмотреть ответы

DevAdmin

1720

пусть точка K середина стороны BC.
AK- медиана/биссектриса/высота в равностороннем треугольнике ABC.
найдем AK:
$AK=AB*sin(60)=AB*\frac{\sqrt }=8\sqrt*\frac{\sqrt } =4*3=12$
----------------------
SK- медиана/биссектриса/высота в равнобедренном треугольнике SBC.
найдем SK:
по теореме пифагора:
$SK=\sqrt}=\sqrt=\sqrt$
$MK=\frac=\frac{\sqrt }$ (так как точка пересечения медиан делит их в отношении 2 к 1)
значит искомый угол равен:
$\alpha =arctg(\frac{\sqrt })$
что приблизительно равно 23,32701352...°

Хороший ответ

4 апреля 2023 17:13

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Найти диагонали правильной шестиугольной призмы, каждое ребро которой равно а. Нашла большую диагональ-2а, как найти вторую? (в ответе а*корень из 5)... Основания трапеции равны 3 и 2. Диагонали её равны 3 и 4. Найти площадь трапеции.... Найти прямую которая образует с CD1 пару скрещивающихся прямых и объяснить.... 8 класс Самостоятельная работа Вариант 2 Тема: «Признаки подобия треугольников» 1) Дано: А=50˚, С=60˚, С1=60˚, В1=70˚. Доказать: ΔАВС ΔА1В1С... Ребяяяят 50 баллов В прямоугольном треугольнике DCE с прямым углом С проведена биссектриса EF, причем FC = 13см. Найти расстояние от точки F до прямой...