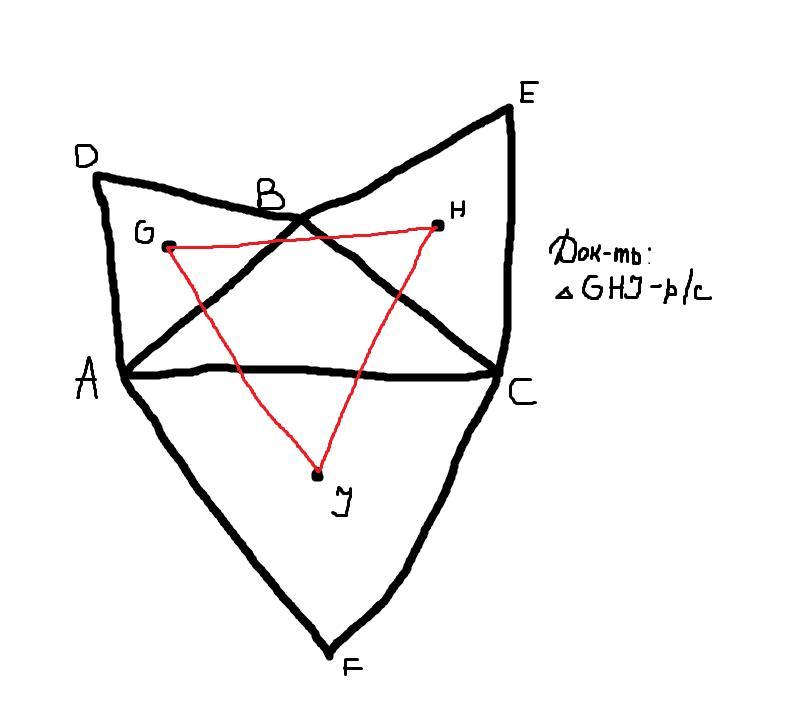
Доказать, что треугольник GHJ равносторонний.

На сторонах треугольника ABC вовне построены равносторонние треугольники. Доказать, что их центры образуют равносторонний треугольник (теорема Наполеона).

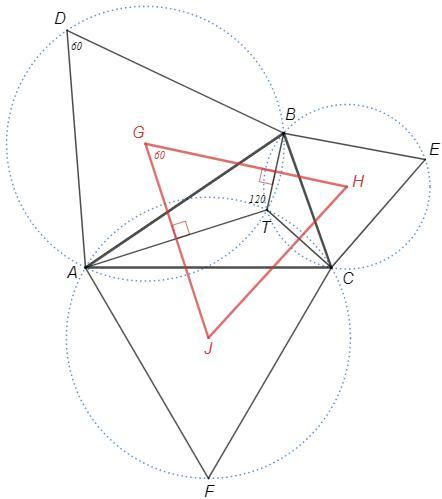
Окружности ADB и BEC вторично пересекаются в точке T.
ADBT, BECT - вписанные четырехугольники.
Сумма углов вписанного четырехугольника 180.
∠ATB =∠BTC =180-60 =120
Тогда ∠ATC =360-120-120 =120
=> AFCT - вписанный четырехугольник (т.к. ∠ATC+∠F=180)
Точка T лежит на окружности AFC.
Линия центров двух окружностей перпендикулярна общей хорде.
GJ⊥AT, GH⊥BT, HJ⊥CT
∠ATB=∠BTC=∠ATC=120 => ∠G=∠H=∠J=60 => △GHJ - равносторонний.