концы отрезка отстоят от плоскости а на расстояниях 12 и 8 см. найдите расстояние от середины отрезка до плоскости а.

1 ответ

Посмотреть ответы

DevAdmin

1720

Ответ:
10 см.
Объяснение:
Искомое расстояние - средняя линия трапеции с основаниями, рваными 12см и 8см. Найдем по формуле: (12+8)/2 =10см.
Или так:
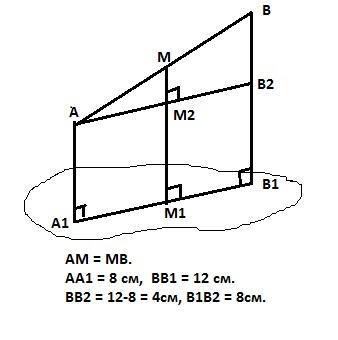
Пусть отрезок АВ, концы отрезка проецируются на плоскость в точки А1 и В1 соответственно. АА1 = 8см,
ВВ1 = 12см. Фигура АВВ1А1 лежит в одной плоскости, пересекающей данную по прямой А1В1.
Проведем прямую АА2 параллельно А1В1. Тогда в прямоугольном треугольнике АВА2 катет ВА2 равен
ВА2 = 12 - 8 = 4 см.
Средняя линия ММ2 этого треугольника равна 2см.
Тогда расстояние от середины отрезка АВ до плоскости равно
ММ1 = ММ2 + М2М1 = 2 + 8 =10см.

Хороший ответ

4 апреля 2023 19:54

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Определение многогранника,его элементы,примеры.... Какое из следующих утверждений верно? 1) Точка пересечения двух окружностей равноудалена от центров этих окружностей. 2) В паралл... Найти углы равнобедренного треугольника, если угол, противолежащий основанию равен 133° Помогите пожалуйста!Срочно!... геометрия 1. Средние линии треугольника относятся как 1:5:8, а периметр треугольник равен 40,5 см. Найдите стороны треугольника. 2. Медианы... Параллельные плоскости альфа и бета пересекают сторону АВ угла ВАС соответственно в точках А1 и А2, а сторону АС этого угла в В1 и В2. Найти АА1 если...