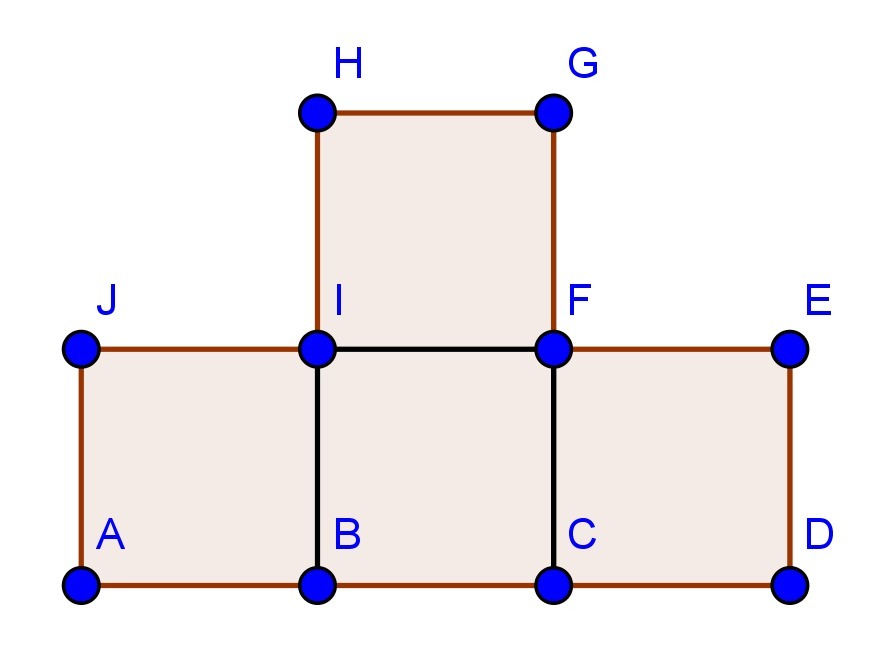
Сколько различных по площади треугольников можно построить так, чтобы их вершины находились в узлах сетки и треугольники полностью лежали внутри фигуры?

У фигуры 3 горизонтальные линии, на них нужно разместить три вершины, чтобы они образовали треугольник. Это возможно, если на каждую горизонталь поставить по 1 вершине или если поставить 2 вершины на одну горизонталь и одну на другую.

1) На каждой горизонтали по вершине.
Исходя из симметрии можно считать, что H — вершина (если G, просто отразим рисунок). Значит, A, E, G и J — не вершины. На второй диагонали остались два узла: F и I.
a. F — вершина. Тогда I и D — не вершины, остаётся два возможных треугольника: HFB (площадь 1) и HFC (площадь 1/2).
b. I — вершина. Тогда F и B — не вершины, оставшиеся треугольники: HIC (площадь 1/2) и HID (площадь 1).

2) На какой-то горизонтали две вершины, на другой одна.
Основание треугольника может быь равно 1, 2 или 3, а высота 1 или 2.
a. Основание 3, тогда высота 1 (2 быть не может: пусть H — вершина, тогда A — не вершина, основание не длиннее BD = 2). Площадь 3 * 1 / 2 = 3/2, пример треугольника ADE.
b. Основание 2, высота 1. Площадь: 2 * 1/2 = 1, пример треугольника: ACJ.
c. Основание 2, высота 2. Площадь: 2 * 2 / 2 = 2, пример треугольника: BDH.
d. Основание 1, высота 1. Площадь 1 * 1 / 2 = 1/2, пример треугольника: ABJ.
e. Основание 1, высота 2. Площадь: 1 * 2 / 2 = 1, пример треугольника: BCH.

Получились площади 1/2, 1, 3/2 и 2 — всего 4 варианта.