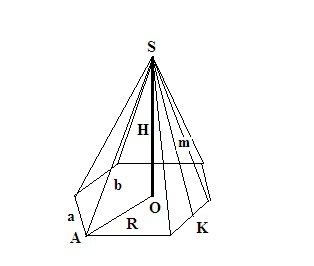
6)найти площадь боковой поверхности правильной шестиугольной пирамиды с высотой 4 дм и боковым ребром 16 дм
С рисунком!

Высота SO = H = 4 дм, боковое ребро AS = b = 16 дм.
По теореме Пифагора
AO^2 = R^2 = b^2 - H^2 = 256 - 16 = 240; R = √240 = 4√15 ~ 15,5 дм.
В правильном 6-угольнике сторона а = R = 4√15 дм.
Боковая поверхность - это 6 одинаковых равнобедренных треугольников.
Апофема SK^2 = m^2 = b^2 - (a/2)^2 = 16^2 - (2√15)^2 = 256 - 60 = 196
SK = m = 14 дм.
Площадь одного треугольника
S(тр) = a*m/2 = 14*4√15/2 = 28√15 ~ 108,44 кв.дм.
Площадь всей боковой поверхности
S = 6*S(тр) = 6*28√15 = 168√15 ~ 650,66 кв.дм.