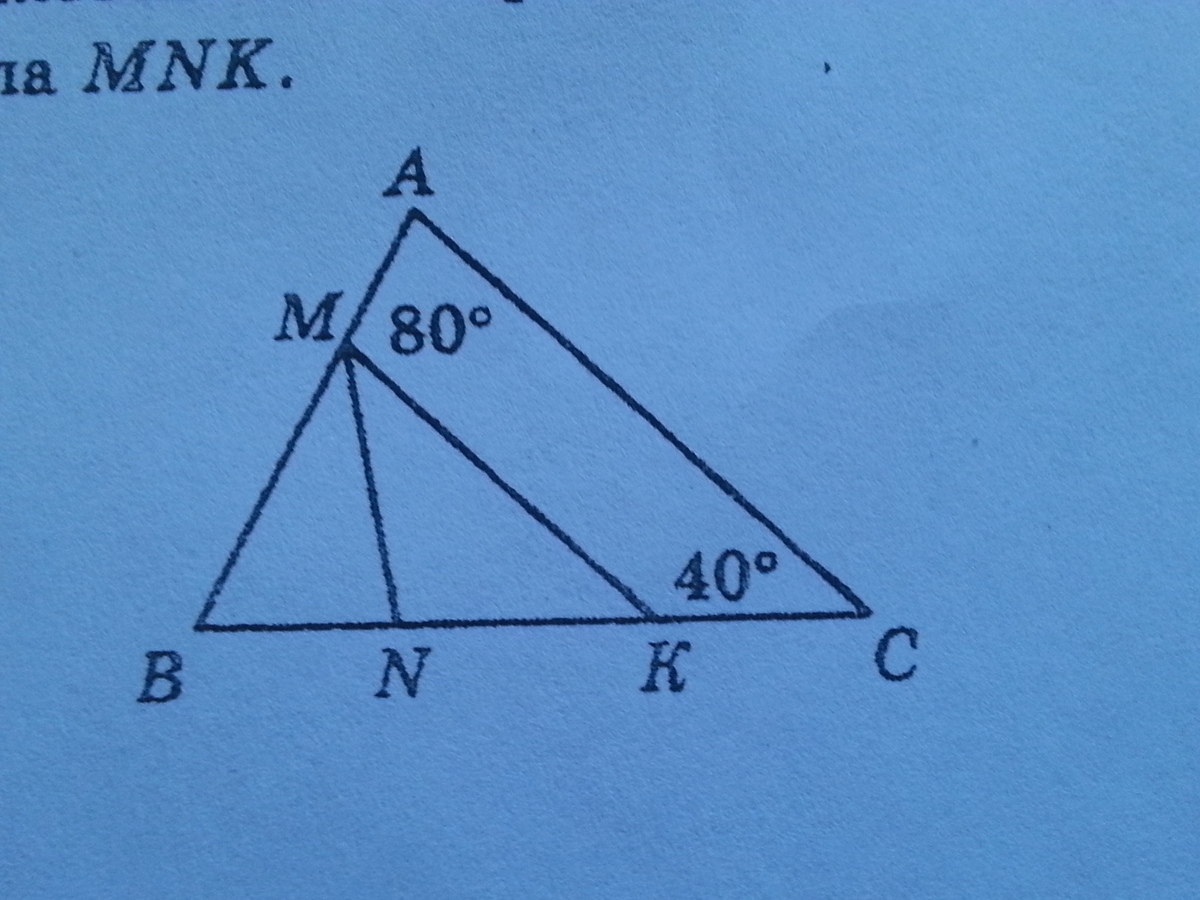
На рисунке отрезок МК параллелен стороне АС. Луч МN является биссектрисой угла ВМК. Найдите величину угла MNK.Заранее спасибо!

1 ответ

Посмотреть ответы

DevAdmin

1720

Решение:
1) Рассмотрим треугольник АВС
По теореме о сумме углов треугольника найдем угол В.
Угол В = 180° - угол А - угол С = 180° - 80° - 40° = 60°
2) Угол ВМK = углу А (соответственные при МК || АС и секущей АВ)
Угол ВМK = 80°
3) Угол ВМN = углу MKN (т.к. MN - биссектриса угла ВМК)
Угол ВМN = углу MKN = 80° : 2 = 40°
4) Рассмотрим треугольник ВМN
По теореме о сумме углов треугольника найдем угол МNВ.
Угол MNB = 180° - угол В - угол ВМN = 180° - 60° - 40° = 80°
5) Сумма углов MNB и MNK равна 180°, т.к. они смешные.
Отсюда угол MNK = 180° - угол MNB = 180° - 80° = 100°
Ответ: угол MNK = 100°

Хороший ответ

5 апреля 2023 06:53

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Помогите решить) Объем конуса равен 16. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего кон... В фирме"Родник"стоимость(в рублях) колодца из железнобетонных колец расчитывается по формуле С=6000+4100*n,где n -число колец ,установленных при рытье... Какое из следующих утверждений верно? 1) Сумма углов выпуклого четырёхугольника равна 360 градусам. 2) Средняя линия трапеции равна сумме её оснований... Доказать теорему если диагонали параллелограмма перпендикулярны , то этот параллелограмм - ромб... В остроугольном треугольнике АВС серединные перпендикуляры  сторон АВ и ВС пересекаются в точке О, ОВ=10 см. Найдите расстояние от  точки...