Лучшие помощники
- Megamozg 2205 б
- Matalya1 1800 б
- DevAdmin 1720 б
- arkasha_bortnikov 900 б
- Dwayne_Johnson 870 б
3 апреля 2023 00:38
1130
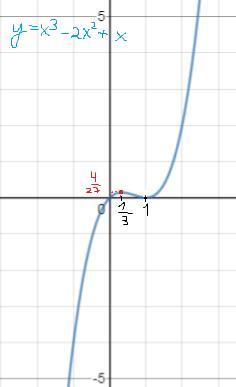
Y=x^3-2x^2+x
Исследуйте функцию и постройте её график
y=x^3-2x^2+x
1
ответ
Ответ:
Объяснение:
1) область определения: х ∈ R. Следовательно, точек разрыва и асимптот у графика нет.
2) исследуем функцию на четность. Вместо х подставляем -х:
y(-x) = (-x)³ - 2(-x)² + (-x) = -x³ - 2x² - x = -(x³ + 2x² + x) ≠ f(x) ≠ -f(x).
Так как ни одно из равенств f(-x) = f(x) и f(-x) = -f(x) не выполняется, функция является ни четной, ни нечетной.
3) Найдем точки пересечения графика функции с осями координат:
с осью ОХ: у = 0; x³ - 2x² + x = 0; x(x² - 2x + 1) = 0; x(x - 1)² = 0 ⇒ x = 0 или x = 1 Искомые точки: (0; 0), (1; 0).
с осью ОУ: х = 0; y(0) = 0³ - 2 · 0² + 0 = 0. Искомая точка - (0; 0).
4) Найдем точки экстремума и экстремумы функции. Для этого сначала найдем производную:
y' = (x³ - 2x² + x)' = (x³)' - (2x²)' + x' = 3x² - 4x + 1.
Ищем критические точки. Таких, что в них производная не существует, у нас нет. Значит, ищем точки, в которых производная равна 0. Решаем уравнение y' = 0:
3x² - 4x + 1 = 0
D = b² - 4ac = (-4)² - 4 · 3 · 1 = 16 - 12 = 4
 .
.
Критические точки - x = 1, x = 1/3. Исследуем их.
При переходе через точку х = 1/3 производная меняет знак с плюса на минус, а при переходе через точку х = 1 - с минуса на плюс. Следовательно х = 1/3 - точка локального максимума, а х = 1 - точка локального минимума.
Ищем локальный минимум и локальный максимум функции. Для этого вместо х в первоначальную функцию подставляем х = 1/3 и х = 1
 - локальный минимум.
- локальный минимум.
 - локальный минимум.
- локальный минимум.
График - во вложении.
Объяснение:
1) область определения: х ∈ R. Следовательно, точек разрыва и асимптот у графика нет.
2) исследуем функцию на четность. Вместо х подставляем -х:
y(-x) = (-x)³ - 2(-x)² + (-x) = -x³ - 2x² - x = -(x³ + 2x² + x) ≠ f(x) ≠ -f(x).
Так как ни одно из равенств f(-x) = f(x) и f(-x) = -f(x) не выполняется, функция является ни четной, ни нечетной.
3) Найдем точки пересечения графика функции с осями координат:
с осью ОХ: у = 0; x³ - 2x² + x = 0; x(x² - 2x + 1) = 0; x(x - 1)² = 0 ⇒ x = 0 или x = 1 Искомые точки: (0; 0), (1; 0).
с осью ОУ: х = 0; y(0) = 0³ - 2 · 0² + 0 = 0. Искомая точка - (0; 0).
4) Найдем точки экстремума и экстремумы функции. Для этого сначала найдем производную:
y' = (x³ - 2x² + x)' = (x³)' - (2x²)' + x' = 3x² - 4x + 1.
Ищем критические точки. Таких, что в них производная не существует, у нас нет. Значит, ищем точки, в которых производная равна 0. Решаем уравнение y' = 0:
3x² - 4x + 1 = 0
D = b² - 4ac = (-4)² - 4 · 3 · 1 = 16 - 12 = 4
Критические точки - x = 1, x = 1/3. Исследуем их.
При переходе через точку х = 1/3 производная меняет знак с плюса на минус, а при переходе через точку х = 1 - с минуса на плюс. Следовательно х = 1/3 - точка локального максимума, а х = 1 - точка локального минимума.
Ищем локальный минимум и локальный максимум функции. Для этого вместо х в первоначальную функцию подставляем х = 1/3 и х = 1
График - во вложении.
0
·
Хороший ответ
5 апреля 2023 00:38
Остались вопросы?
Еще вопросы по категории Алгебра
|x-4|=0 как это правильно решить?...
Задание В11: Цилиндр описан около шара. Объем цилиндра равен 33. Найдите объем шара....
внутри равнобедренного треугольника АВС с основанием ВС отмечена точка Д так,что АД=ДС. известно что угол ВАД=А и угол ДАС=3а. найдите а...
Последовательность задана формулой bn=n^2+3. найдите ее четвертый член...
Срочно! Дана геометрическая прогрессия (cn) ∶ c4 = 20, q = 2. Найди c7. онлайн мектеп! Ответ: ...