Лучшие помощники
- Megamozg 2205 б
- Matalya1 1800 б
- DevAdmin 1720 б
- arkasha_bortnikov 900 б
- Dwayne_Johnson 870 б
3 апреля 2023 00:48
636
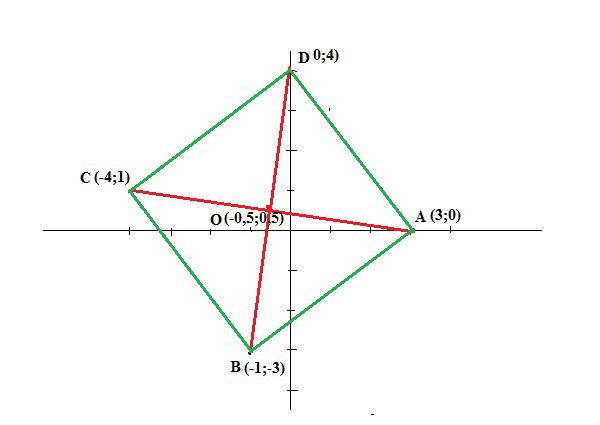
Даны две противоположные вершины квадрата А(3;0) и С(-4; 1). Найти две его другие вершины
1
ответ
Найдем координаты вектора АС (диагональ квадрата) и его модуль.
Координаты вектора равны разности соответствующих координат точек его конца и начала. Длина вектора (модуль), заданного координатами, равна корню квадратному из суммы квадратов его координат.
В нашем случае: АС{-7;1} и |AC|=√(49+1)=√50.
Нам дан квадрат. Его стороны равны. Значит |AB|=|BC|=5. (по Пифагору).
Пусть вершина В квадрата имеет координаты Хb и Yb.
Тогда координаты вектора АВ,
а координаты вектора СВ.
Их модули соответственно
|AB|=√[(Xb-3)²+Yb²)] и |СВ|=√[(Xb-4)²+(Yb-1)²] равны между собой и равны 5.
Равны и квадраты модулей, то есть:
Xb²-6Xb+9+Yb²=Xb²-8Xb+16+Yb²-Yb+1 или 14Xb-2Yb+8=0 отсюда Yb=7Xb+4.
Так как квадрат модуля АВ равен 25, имеем:
Xb²-6Xb+9+(7Xb+4)²=25. Отсюда Xb²-6Xb+9+49Xb²+56Xb+16-25=0. Отсюда Х1=-1 и X2=0 (не удовлетворяет). Итак, точка В имеет координаты Xb=-1 и Yb=7*(-1)+4=-3.
То есть имеем: В(-1;-3).
найдем координаты точки О пересечения диагоналей. Это точка О - середина диагонали АС (свойство диагоналей).
Координаты середины отрезка AС равны сумме координат начала и конца отрезка, деленной пополам. то есть О((3-4)/3;(1+0)/2) или О(-0,5;0,5).
По этой же формуле Xo=(Xb+Xd)/2 и Yo=(Yb+Yd)/2. Подставим известные значения и получим: Xd=0 и Yd=4.
Ответ: вершины квадрата АВСD имеют координаты В(-1;-3) и D(0;4).
Координаты вектора равны разности соответствующих координат точек его конца и начала. Длина вектора (модуль), заданного координатами, равна корню квадратному из суммы квадратов его координат.
В нашем случае: АС{-7;1} и |AC|=√(49+1)=√50.
Нам дан квадрат. Его стороны равны. Значит |AB|=|BC|=5. (по Пифагору).
Пусть вершина В квадрата имеет координаты Хb и Yb.
Тогда координаты вектора АВ,
а координаты вектора СВ.
Их модули соответственно
|AB|=√[(Xb-3)²+Yb²)] и |СВ|=√[(Xb-4)²+(Yb-1)²] равны между собой и равны 5.
Равны и квадраты модулей, то есть:
Xb²-6Xb+9+Yb²=Xb²-8Xb+16+Yb²-Yb+1 или 14Xb-2Yb+8=0 отсюда Yb=7Xb+4.
Так как квадрат модуля АВ равен 25, имеем:
Xb²-6Xb+9+(7Xb+4)²=25. Отсюда Xb²-6Xb+9+49Xb²+56Xb+16-25=0. Отсюда Х1=-1 и X2=0 (не удовлетворяет). Итак, точка В имеет координаты Xb=-1 и Yb=7*(-1)+4=-3.
То есть имеем: В(-1;-3).
найдем координаты точки О пересечения диагоналей. Это точка О - середина диагонали АС (свойство диагоналей).
Координаты середины отрезка AС равны сумме координат начала и конца отрезка, деленной пополам. то есть О((3-4)/3;(1+0)/2) или О(-0,5;0,5).
По этой же формуле Xo=(Xb+Xd)/2 и Yo=(Yb+Yd)/2. Подставим известные значения и получим: Xd=0 и Yd=4.
Ответ: вершины квадрата АВСD имеют координаты В(-1;-3) и D(0;4).
0
·
Хороший ответ
5 апреля 2023 00:48
Остались вопросы?
Еще вопросы по категории Геометрия
Ребра тетраэдра равны 38. Найдите площадь сечения, проходящего через середины четырех его ребер....
определить острые углы прямоугольного треугольника , если отношение радиусов описанной и вписанной окружностей равно √(3) + 1....
Основания трапеции равны 10 и 11 найдите больший из отрезков на которые делит среднюю линию этой трапеции одна из ее диагоналей...
найдите градусную меру углов,которые получаются при пересечении двух прямых,если сумма трёх из этих углов равна 270 градусов...
В треугольнике со сторонами 12 и 3 проведены высоты к этим сторонам. Высота, проведенная к первой стороне, равна 1. Чему равна высота проведенная ко в...