1. Неравенство треугольника (доказать).

Теореме о неравенстве треугольника:
Длина любой стороны треугольника меньше суммы двух других его сторон.
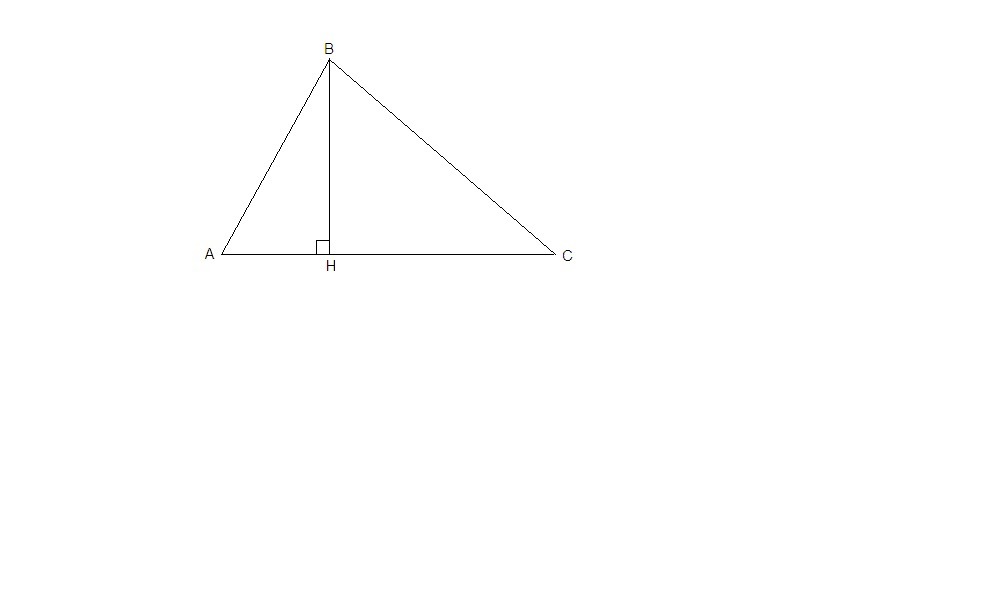
Пусть АС - большая сторона треугольника.
Докажем, что АС < AB + BC.
Опустим высоту ВН на сторону АС.
В треугольнике напротив большего угла лежит большая сторона. В прямоугольном треугольнике прямой угол - самый большой, напротив него лежит гипотенуза, значит катет всегда меньше гипотенузы.
ΔАВН: АН < AB
ΔCBH: CH < BC, складываем неравенства и получаем:
АН + СН < AB + BC или
AC < AB + BC.

Так как теорема доказана для большей стороны, для двух других сторон она очевидно верна.