Составить уравнение касательной y=ctgx при х 0=п/6. заранее спасибо!

1 ответ

Посмотреть ответы

DevAdmin

1705

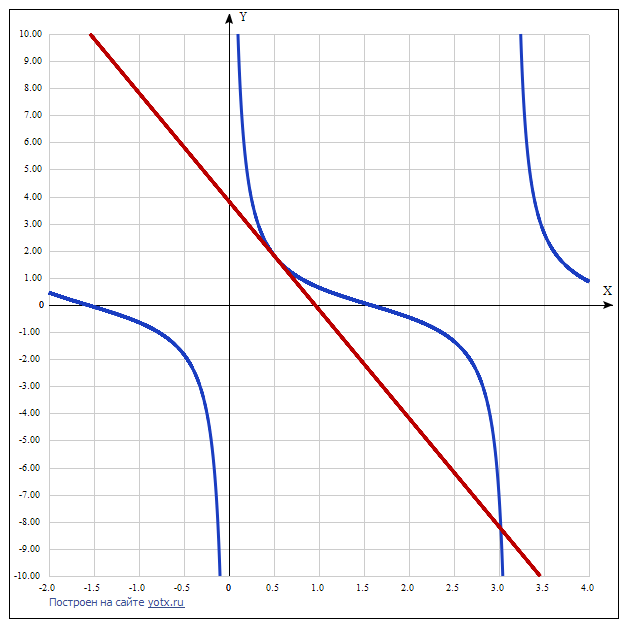
Уравнение касательной:
y' = f'(Xo)*(X-Xo) + f(Xo).
y'(X)=f'(ctg(X) = -1 / (sin²(X)).
y'(Xo) = -1 / (sin²(pi/6)) = -1 / ((1/2)²) = -1 / (1/4) = -4.
f(Xo) = ctg(pi/6) = √3.
Подставляем полученные значения:
y' = -4(X - (pi/6)) + √3 =
= -4X + (4*pi/6) + √3 =
= -4X + (2pi/3) + √3 = -4X + 3.826446

Хороший ответ

5 апреля 2023 01:07

Остались вопросы?

Найти нужный

Еще вопросы по категории Алгебра

Сколько корней имеет уравнение x2-2x+8 ______ =0 x-4... Решить уравнение x^4=20... две соревнующиеся бригады рабочих должны были изготовить по 240 деталей. первая бригада изготовляла в день на 8 деталей больше чем вторая и в результа... Найти корень уравнения (x-3)^9=512... 7. На встрече выпускников 9 бывших одноклассников обменялись визитками. Сколько было использовано визиток?...