Лучшие помощники
- Megamozg 2205 б
- Matalya1 1800 б
- DevAdmin 1720 б
- arkasha_bortnikov 900 б
- Dwayne_Johnson 870 б
15 декабря 2022 23:31
1231
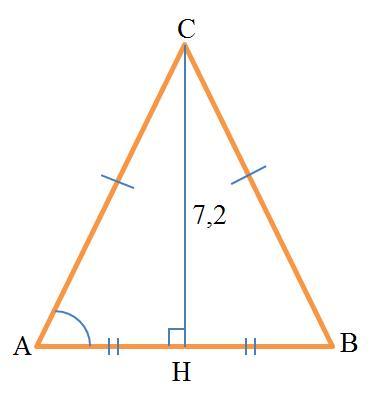
В треугольнике ABC AC = BC, высота CH равна 7,2 и cosA=4/5 . Найдите AC.
1
ответ
Ответ:
12 (единиц)
Объяснение:
Дано:
ΔABC (см. рисунок)
AC=BC
CH⊥AB
CH=7,2
cos∠A=4/5
Найти AC.
Решение.
Так как AC=BC, то ΔABC равнобедренный. Тогда углы ∠A и ∠B при основании равны, следовательно острые. Поэтому sin∠A > 0.
Далее, из cos∠A=4/5 получаем, что
sin∠A=√(1-cos²∠A) = √(1-16/25) = √(9/25) = 3/5.
С другой стороны sin∠A= CH/AC .
Отсюда
AC = CH/sin∠A = 7,2/(3/5) = (5∙7,2)/3 = 36/3 = 12 (единиц).
12 (единиц)
Объяснение:
Дано:
ΔABC (см. рисунок)
AC=BC
CH⊥AB
CH=7,2
cos∠A=4/5
Найти AC.
Решение.
Так как AC=BC, то ΔABC равнобедренный. Тогда углы ∠A и ∠B при основании равны, следовательно острые. Поэтому sin∠A > 0.
Далее, из cos∠A=4/5 получаем, что
sin∠A=√(1-cos²∠A) = √(1-16/25) = √(9/25) = 3/5.
С другой стороны sin∠A= CH/AC .
Отсюда
AC = CH/sin∠A = 7,2/(3/5) = (5∙7,2)/3 = 36/3 = 12 (единиц).
0
·
Хороший ответ
17 декабря 2022 23:31
Остались вопросы?
Еще вопросы по категории Алгебра
Биссектриса параллелограмма делит противолежащую сторону на части 8см и 6 см. Найдите периметр параллелограмма...
...
В комнате находятся 100 человек, каждый из которых либо рыцарь, который говорит правду, либо лжец, который всегда лжёт. Все они разного роста. Каждый...
Разложите на множители : 1) 100-a² 2) x²+10x+25 3) 36y²-49 4) 16a²-24ab+9b2...
На рисунке изображён график прямой. Напишите формулу которая задаёт эту прямую. ...