найдите стороны равнобедренного треугольника, если его периметр =54 см, а высота, проведенная к основанию, - 9 см

1 ответ

Посмотреть ответы

DevAdmin

1720

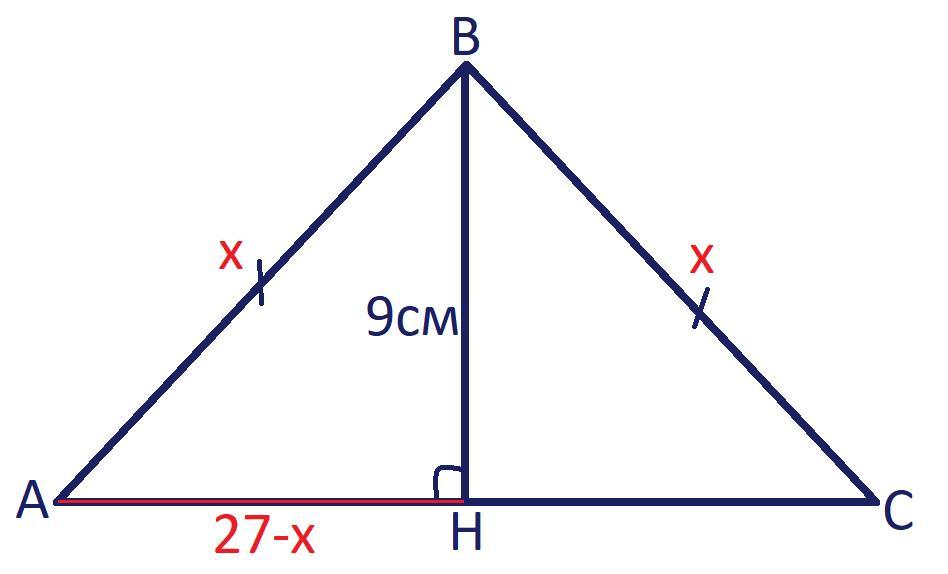
Дано: △ABC - равнобедренный (AB=CB); BH - высота; BH = 9см; P(ABC) = 54см.
Найти: AB, BC, AC.
Решение:
Пусть AB = x см.
P(ABC) = AB+BC+AC;
AC = P(ABC)-2·AB;
AC = 54-2x см.

Высота равнобедренного треугольника, проведённая к его основанию, является так же медианой.

⇒ AH = HC = AC:2 = (54-2x):2 = 27-x см;
△AHB - прямоугольный (∠H=90°), тогда по теореме Пифагора получим:
AB² = AH²+BH²;
x² = (27-x)²+9²;
x² = 27²-54x+x²+9²;
54x = 3²·9²+9² = 10·81;
54x = 2·5·3·27;
x = $\dfrac =3\cdot 5=15$
AB = 15см;
BC = AB = 15см;
AC = 54-2·15 = 54-30 = 24 см.
Ответ: 15см, 15см и 24см.

Хороший ответ

5 апреля 2023 01:40

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

помогите 8 класс. CE - биссектриса параллелограмма ABCD . Точка E лежит на стене AD , ED = 3, AE = 5. Найдите периметр параллелограмма.... Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличиться на 54.Найдите ребро куба.... сторона правильного четырехугольника, вписанного в некоторую окружность, равна 2. найти сторону правильного треугольника, описанного около этой окружн... Биссектриса BD делит сторону AC треугольника ABC на отрезки AD и CD, равные соответственно 7 см и 10,5 см, AB=9 см. Найдите периметр треугольника ABC... Верно ли следующее утверждение: прямая, пересекающая одну из расположенных в пространстве параллельных прямых пересекает и другую. Поясните...