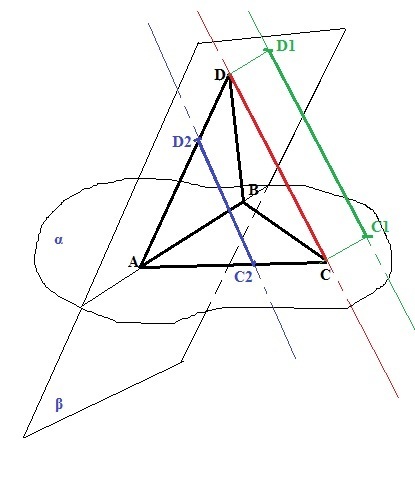
Треугольники ABC и ABD не лежат в одной плоскости. Докажите, что любая прямая, параллельная отрезку CD, пересекает плоскости данных треугольников.(рисунок желателен)

Есть теорема: "Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость". Отрезок CD имеет общую точку C с плоскостью АВС и общую точку D с плоскостью ABD. Через две точки можно провести только одну прямую, следовательно, прямая, содержащая отрезок СD, пересекает плоскость, содержащую треугольник АВС и плоскость, содержващую треугольник ABD. Значит любая прямая, параллельная СD, по приведенной теореме, также пересечет и плоскость АВС и плолскость ABD. Что и требовалось доказать.