помогите решить задачи про шестиугольную пирамиду 1) В правильной шестиугольной пирамиде SABCDEF сторонаоснования равна корень из 3, а боковое ребро равно 2. Найдите угол SAD. 2) В правильной шестиугольной пирамиде SABCDEF сторона основания равна 1, а высота равна корень из 3. Найдите угол между высотой и боковым ребром. 3) В правильной шестиугольной пирамиде SABCDEF сторона основания равна корень из 3, а боковое ребро равно 3. Найдите угол SAC. 4) В правильной шестиугольной пирамиде сторона основания равна апофеме. Найдите угол между боковой гранью и основанием.

Ответ:
1) ∠SAD = 30°.
2) ∠ASO = 30°.
3) ∠SAC = 60°.
4) ∠SHO = 30°.
Объяснение:
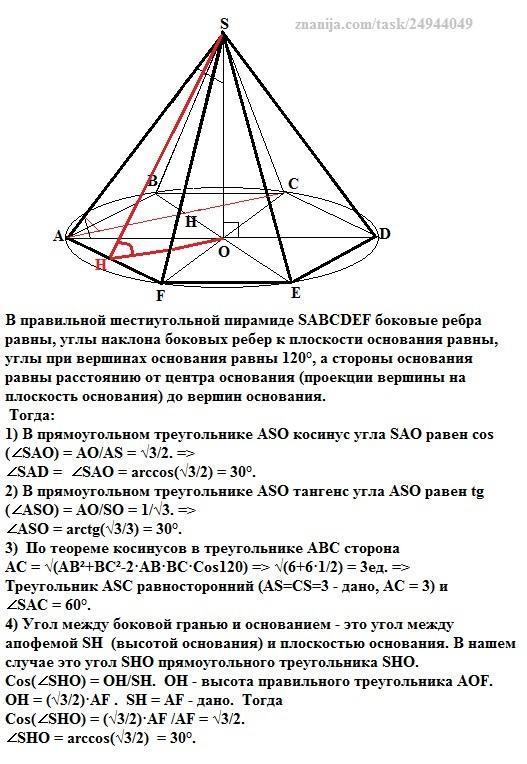
В правильной шестиугольной пирамиде SABCDEF боковые ребра равны, углы наклона боковых ребер к плоскости основания равны, углы при вершинах основания равны 120°, а стороны основания равны расстоянию от центра основания (проекции вершины на плоскость основания) до вершин основания.
Тогда:
1) В прямоугольном треугольнике АSО косинус угла SAO равен сos(∠SAO) = АО/AS = √3/2. =>
∠SAD = ∠SAO = arccos(√3/2) = 30°.
2) В прямоугольном треугольнике АSО тангенс угла АSO равен tg(∠ASO) = АО/SO = 1/√3. =>
∠ASO = arctg(√3/3) = 30°.
3) По теореме косинусов в треугольнике АВС сторона
АС = √(АВ²+ВС²-2·АВ·ВС·Cos120) => √(6+6·1/2) = 3ед. =>
Треугольник АSС равносторонний (AS=CS=3 - дано, АС = 3) и
∠SAC = 60°.
4) Угол между боковой гранью и основанием - это угол между апофемой SH (высотой основания) и плоскостью основания. В нашем случае это угол SHO прямоугольного треугольника SHO.
Cos(∠SHO) = OH/SH. OH - высота правильного треугольника AOF.
OH = (√3/2)·AF . SH = AF - дано. Тогда
Cos(∠SHO) = (√3/2)·AF /AF = √3/2.
∠SHO = arccos(√3/2) = 30°.