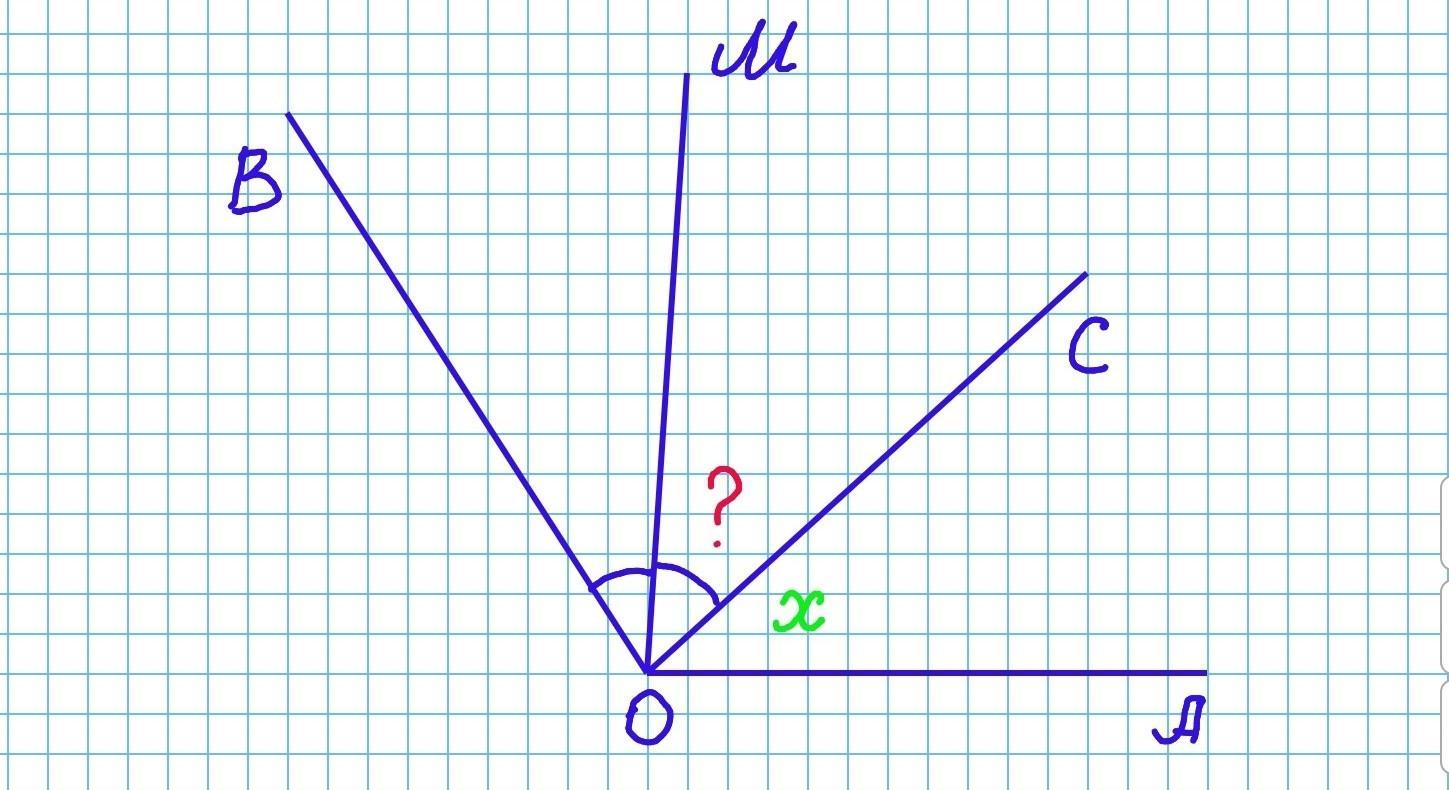
Между сторонами угла АОВ, равного 140°, проведены лучи ОС и ом так, что угол АОСна 16° меньше угла ВОС, а OM — биссектриса угла Вос. Найдите величину угла COM.
Ответ дайте в градусах.
Запишите решение и ответ.

1 ответ

Посмотреть ответы

Megamozg

2200

Ответ:
∠СОМ=39°
Объяснение:
Дано: ∠AOВ=140°, ОМ - биссектриса
Найти: ∠СОМ
Пусть угол АОС равен х градусов, тогда угол ВОС равен х+16°. Так как сумма этих углов равна углу АОВ, составляем уравнение:
∠АОС+∠ВОС=∠AOВ
х+х+16=140
2х=140-16
2х=124
х=62

∠АОС=62°, ∠ВОС=62°+16°=78°.

Так как ОМ - биссектриса ∠ВОС, то по свойству биссектрисы:
∠СОМ=½•∠ВОС=½•78°=39°.

Величина угла СОМ равна 39°.

Хороший ответ

5 апреля 2023 03:49

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

В треугольнике MNK, O - точка пересечения медиан. Выразите вектор NO через векторы a=NM и b=KM.... Объём конуса равен 16. Через середину высоты конуса проведена плоскость, параллельная основанию. Найдите объём конуса, отсекаемого от данного конуса п... на сторонах угла ВАС и на его биссектрисе отложены равные отрезки АВ, АС и АD. Величина угла ВDС равна 160 градусов. Определите величину угла ВАС... Прямая, параллельная стороне АС треугольника АВС, пересекает стороны АВ и ВС в точках М и N соответственно, АС = 16, МN = 10. Площадь треугольника АВС... Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, которые равны 4 см и 3 см , считая от...