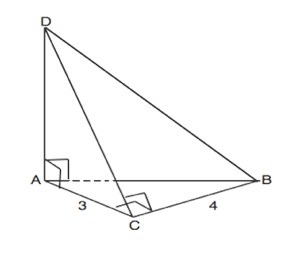
Дан тетраэдр abcd, ad перпен. ac, ad перпенд. ab, dc перпенд. cb, bc=4, ac=3. Докажите, что ad перпенд. bc, bc перпендик.(adc) и найти площадь Abc

1 ответ

Посмотреть ответы

Megamozg

2190

Дано: АD⊥АС, АD ⊥АВ. Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна этой плоскости.
Следовательно, АD перпендиулярна плоскости АВС.
Если прямая перпендикулярна к плоскости, то она перпендикулярна к любой прямой, лежащей в этой плоскости.⇒
АD⊥ВС
Наклонная DС⊥ВС по условию, АС - проекция DС на плоскость АВС. По т. о 3-х перпендикулярах АС⊥ВС, и ∆ АВС прямоугольный с прямым углом АСВ.
ВС⊥DC ( дано), ВС⊥АС ( найдено). ⇒ ВС перпендикулярна двум пересекающимся прямым в плоскости ADC, следовательно, ВС перпендикулярна плоскости АDC.
Площадь прямоугольного ∆ АВС=АС•ВС:2=3•4:2=6 (ед. площади)

Хороший ответ

5 апреля 2023 05:21

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

ab и cd диаметры окружности.дуга AC=64 найти угол DCB=?... ABCD-параллелограмм. EC=3, AB=7, Найти площадь параллелограмма. Варианты ответов: A) 7 B) 10 C) 14 D) 21 E) 28 (Нужно решение)... Помогите пожалуйста... В треугольнике ABC AC=BC AB=8 cos A=0,2 найдите AC. Напишите поподробней, плиз!... СРОЧНО 40 Б Один из углов равнобедренного тупоугольного треугольника на 48° меньше другого. Найдите больший угол этого треугольника С решением...