Лучшие помощники
- Megamozg 2205 б
- Matalya1 1800 б
- DevAdmin 1720 б
- arkasha_bortnikov 900 б
- Dwayne_Johnson 870 б
3 апреля 2023 06:34
1158
Два квадрата имеют общую вершину. Найдите отношение отрезков ab и cd, показанных на рисунке
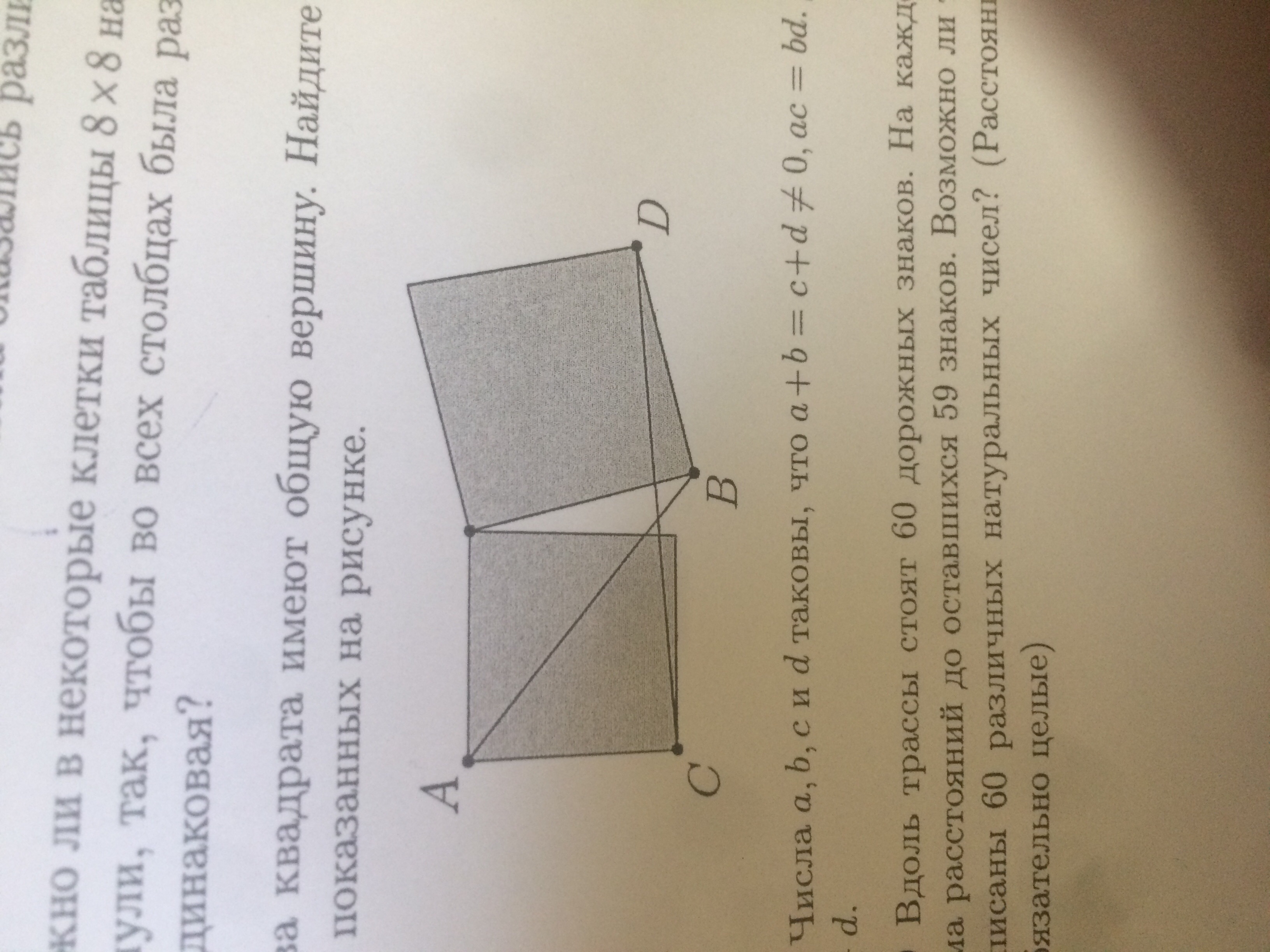
1
ответ
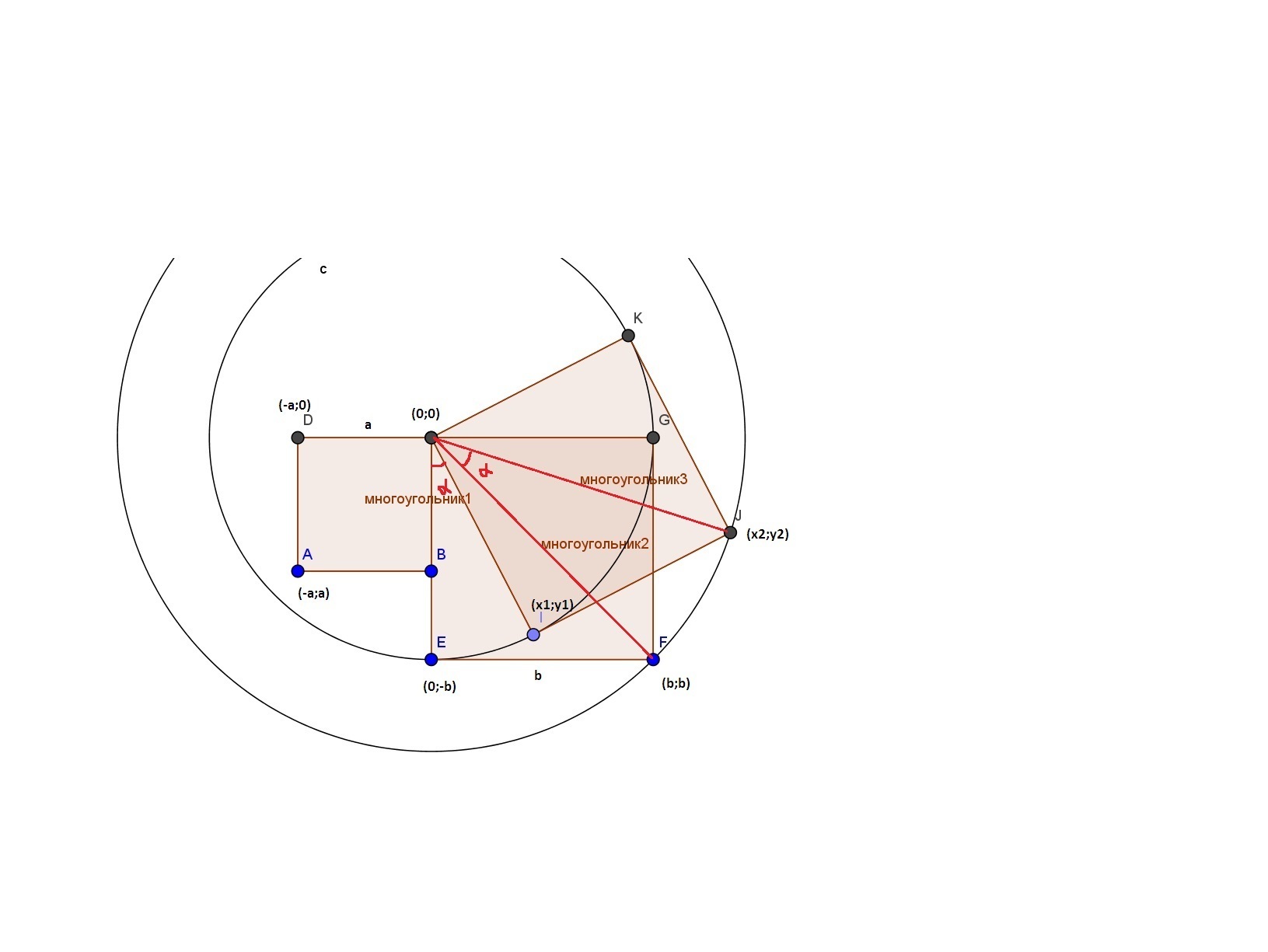
Смотри файл , а потом решение.
Примем стороны квадратов за а и b
Выберем начало координат.
Обозначим координаты точек.
Из рисунка видно, что бОльший квадрат получается поворотом вокруг начала координат
Т.е. точка (х1;у1) получается поворотом на угол α из т. Е, а т.(х2;у2) из т.F
Координаты точек при повороте на угол α вычисляются по формулам
(если их не знать, то задачу можно решить по-другому, но тоже не сложно)
Х'=xcosα-ysinα
Y’=xsinα+ycosα
Т.е. точки (х1;у1) =(bsinα; -bcosα)
(x2;y2)=(bcosα+bsinα; bsinα-bcosα)
Ну , расстояние между точками (х1;у1) и (-а:0)
И точками (х2;у2) и (-а;-а) находится по известной формуле
Когда все подставим, возведем в квадрат и преобразуем, то отношение большего отрезка к меньшему получится равным √2
P.S. формулу расстояния и преобразование не пишу, т.к. задача дана из всеросс. Олимпиады, а там не знающим этих формул делать нечего….
Примем стороны квадратов за а и b
Выберем начало координат.
Обозначим координаты точек.
Из рисунка видно, что бОльший квадрат получается поворотом вокруг начала координат
Т.е. точка (х1;у1) получается поворотом на угол α из т. Е, а т.(х2;у2) из т.F
Координаты точек при повороте на угол α вычисляются по формулам
(если их не знать, то задачу можно решить по-другому, но тоже не сложно)
Х'=xcosα-ysinα
Y’=xsinα+ycosα
Т.е. точки (х1;у1) =(bsinα; -bcosα)
(x2;y2)=(bcosα+bsinα; bsinα-bcosα)
Ну , расстояние между точками (х1;у1) и (-а:0)
И точками (х2;у2) и (-а;-а) находится по известной формуле
Когда все подставим, возведем в квадрат и преобразуем, то отношение большего отрезка к меньшему получится равным √2
P.S. формулу расстояния и преобразование не пишу, т.к. задача дана из всеросс. Олимпиады, а там не знающим этих формул делать нечего….
0
·
Хороший ответ
5 апреля 2023 06:34
Остались вопросы?
Еще вопросы по категории Геометрия
Найдите высоту треугольника АВС, опущенную на сторону ВС, если стороны квадратных клеток равны √2. Пожалуйста!...
объясните, как построить сечение тетраэдра плоскостью, проходящей через данные точки М, N, К и в задачах 1-3 найти периметр сечения, если М, N, К – се...
Найдите площадь кругового сектора,если градусная мера его дуги равна 120,а радиус круга равен 12см...
140 градусов -это какой угол острый тупой или прямой?...
В Кубе ABCDA1B1C1D1 найдите угол между прямыми BA1 и AC. Ответ дайте в градусах....