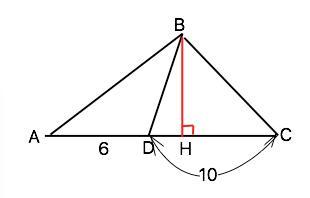
На стороне AC треугольника ABC отмечена точка D так, что AD=6, DC=10. Площадь треугольника ABC равна 48. Найдите площадь треугольника BCD.

1 ответ

Посмотреть ответы

Megamozg

2205

Ответ: 30см²
Объяснение:
Высота ВН общая для треугольников АВС, АВD и BDC.
Если два треугольника имеют одинаковые высоты, то отношение их площадей равно отношению длин оснований (сторон, на которые опущены эти высоты.
Ѕ(ABC):S(BCD)=AC:DC
Примем площадь ∆ BCD равной x ⇒
48:х=(6+10):10 => 480=16х ⇒ х=30 см²
Ответ: Ѕ(BCD)=30 см²
Тот же результат получим из отношения площадей треугольников АВС и BCD, выраженных по формуле S=a•h/2

Хороший ответ

28 декабря 2022 21:53

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Ребяяяят 50 баллов В прямоугольном треугольнике DCE с прямым углом С проведена биссектриса EF, причем FC = 13см. Найти расстояние от точки F до прямой... Луч ОС делит угол АОВ на два угла. Как найди градусную меру угла АОВ, если известны градусные меры углов АОС и СОВ?... Через точку данной окружности проведены касательная и хорда,равная радиусу.Найдите угол между ними. Заранее благодарен :)... Изобразите на окружности числа: 1)П/2+2Пк 2)7П/6+2Пк 3)3п/4+2Пк 4)-П/3+2Пк 5)4П/3+2Пк,К(принадлежит)Z нарисуйте на окружности... 1.Угол DCL = 126(градусов),CM - биссектриса этого угла.Найти угол MCL 2.Найдите длины отрезков BP и DP,если BD = 18 см и отрезок DP на 4 см больше отр...