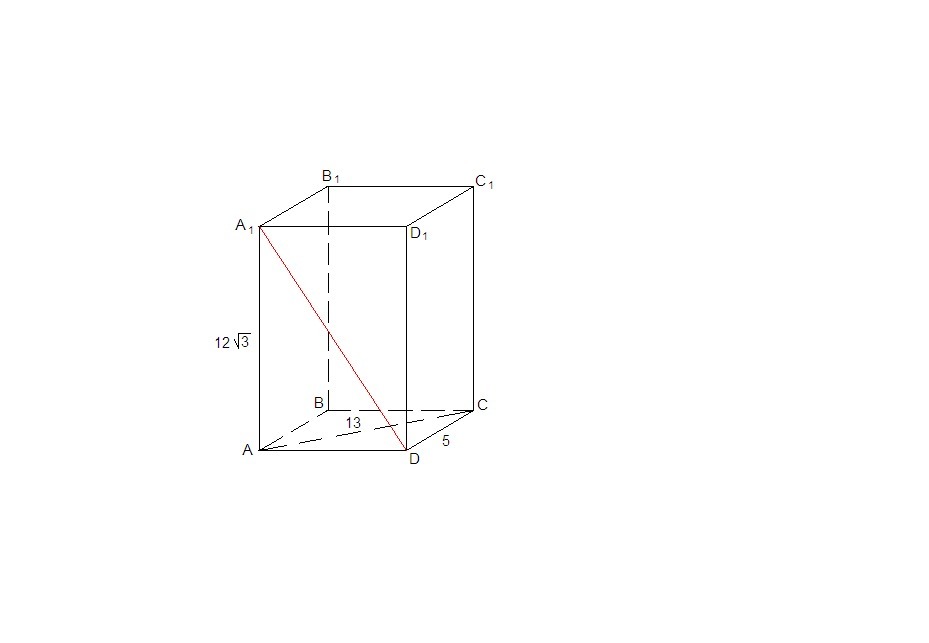
Дан прямоугольный параллелепипед ABCDA1B1C1D1. Найдите двугранный угол A1DCA,если AC=13 см, DC=5 см, AA1=12корень из 3

1 ответ

Посмотреть ответы

m.pozharskiy

AD⊥CD так как все грани прямоугольного параллелепипеда - прямоугольники,
AD - проекция AD₁ на плоскость основания, значит
AD₁⊥CD по теореме о трех перпендикулярах.
∠A₁DA - линейный угол двугранного угла A₁DCA - искомый.

ΔACD: по теореме Пифагора
AD = √(AC² - CD²) = √(169 - 25) = 12

ΔA₁DA: tg∠A₁DA = AA₁ / AD = 12√3 / 12 = √3

∠A₁DA = 60°

Хороший ответ

1 сентября 2022 21:07

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

В треугольнике ABC AB=BC=95, AC=114 . Найдите длину медианы BM .... В окружности с центром О АС и ВД - диаметры.Угол АСВ равен 26 градусов.Найдите Угол АОД . Ответ дайте в градусах,... Чему равен угол альфа, если известно, что: 1) cos альфа = 0,5 2) sin альфа = √2 2 3) tg альфа = √3... Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y=x-17 или совпадает с ней. Подробней на картинке.... Найдите радиус шара описанного около правильной треугольной пирамиды, в которой боковое ребро составляет угол 30 градусов с плоскостью основания, а дл...