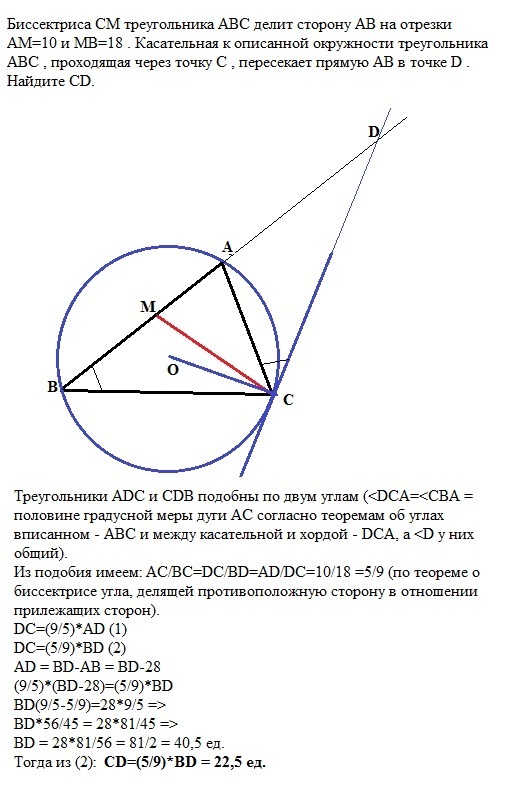
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=10 и MB=18 . Касательная к описанной окружности треугольника ABC , проходящая через точку C , пересекает прямую AB в точке D . Найдите CD .

1 ответ

Посмотреть ответы

DevAdmin

1720

Треугольники ADC и CDB подобны по двум углам (<DCА=<CВА = половине градусной меры дуги АС согласно теоремам об углах вписанном - АВС и между касательной и хордой - DCA, а <D у них общий).
Из подобия имеем: АС/ВС=DC/BD=AD/DC=10/18 =5/9 (по теореме о биссектрисе угла, делящей противоположную сторону в отношении прилежащих сторон - АС/ВС=АМ/МВ).
Тогда из этих соотношений:
DC=(9/5)*AD (1)
DC=(5/9)*BD (2).
АВ=28 (дано), AD = BD-AB = ВD-28.
Приравняем (1) и (2):
(9/5)*(ВD-28)=(5/9)*BD
BD(9/5-5/9)=28*9/5 =>
BD*56/45 = 28*81/45 =>
BD = 28*81/56 = 81/2 = 40,5 ед.
Тогда из (2): СD=(5/9)*BD = 22,5 ед.

Хороший ответ

5 апреля 2023 11:34

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Найдите углы прямоугольной трапеции,если больший из них равен 120 градусов... Дано: NM параллельно AC AM=6см BM=8см AC=21 см а) доказать, что произведение Ab*Bn=CB*BM б) найти MN рисунок во вложенном файле... На продолжении стороны AB равнобедренного треугольника ABC с основанием AC отметили точку D так, что AD = AC и точка A находится между точками B и D.... Помоогите срочно Биссектриса равностороннего треугольника равна половине стороны треугольника.Это утверждение... 1.может быть верно 2.верно всегда 3.н... Сторона ромба равна 1, острый угол равен 30. Найдите радиус вписанной окружности этого ромба...