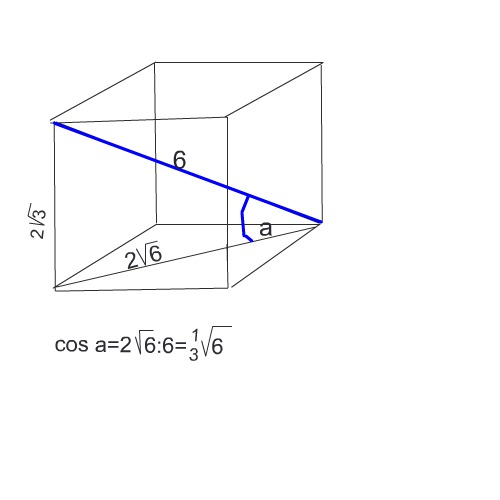
Диагональ куба равна 6 см. Найти: а) ребро куба, б) косинус угла между диагональю куба и плоскостью одной из ее граней. Желательно с чертижем..

2 ответа

Посмотреть ответы

m.pozharskiy

Диагональ куба находится по формуле
а²+2а² =36, где а - ребро куба.
Отсюда
3а² =36, ребро куба = √12=2√3
Косинус а = диагональ основания а√2 ( прилежащий катет) разделить на диагональ куба (гипотенузу).
а√2=2√3*√2=2√6
2√6:6=⅓√6=√6:3

Хороший ответ

1 сентября 2022 21:26

v.petrogradov

диагональ найдем по формуле
a^2+b^2+c^2=36
так как куб=> 3*a^2=36
a^2=12
a=2(корня из трех)
2)cosA=прилижащий катет /на гипотенузу (угол A это угол между наклонной и проецией)
сosA=2(корня из трех)*(корень из двух)/6
cosA=(корень из 6)/3

1 сентября 2022 21:26

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

на рисунке 261 две окружности имеют общий центр о к меньшей из них провели перпендикулярные касательные ab и cd пересекающиеся в точке k найдите радиу... Найти катеты прямоугольного треугольника,если гипотенуза равна 4 см,а косинус одного из углов 0,6.... докажите,что если данная прямая параллельна прямой,по которой пересекаются две плоскости ,и не лежит в этих плоскостях ,то она параллельна этим плоско... Диагональ прямоугольника ABCD равна 16,угол CBD равен альфа .найдите сторону BC.... В треугольнике АВС угол С равен 90 градусов, АС = 15, tgA = 7/15. Найдите BC. Подробное решение, пожалуйста....