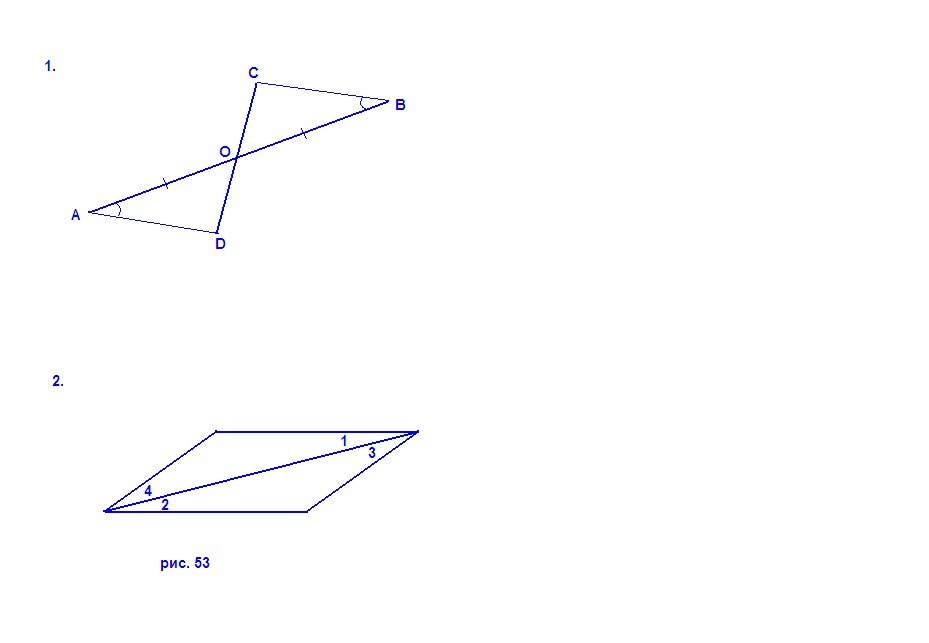
121 Отрезки АВ и CD пересекаются в середине О отрезка АВ, ∠OAD = ∠OBC. а) Докажите, что ΔСВО=ΔDAO; б) найдите ВС и СО, если CD=26 см, AD= 15 см.и 122 На рисунке 53 (с. 31) ∠1 = ∠2, ∠3 = ∠4. а) Докажите, что ΔАВС=ΔCDА; б) найдите АВ и ВС, если AD= 19 см, CD=11 см.

1 ответ

Посмотреть ответы

DevAdmin

1690

121.
а) АО = ОВ по условию,
∠OAD = ∠OBC по условию,
∠AOD = ∠BOC как вертикальные, ⇒
ΔDАО = ΔCВО по стороне и двум прилежащим к ней углам.

б) В равных треугольниках напротив равных углов лежат равные стороны.
ВС = AD = 15 см
СО = OD = CD/2 = 26/2 = 13 см

122.
а) ∠1 = ∠2 по условию,
∠3 = ∠4 по условию,
АС - общая сторона для треугольников АВС и CDA, ⇒
ΔАВС = ΔCDA по стороне и двум прилежащим к ней углам.

б) Из равенства треугольников следует, что
АВ = CD = 11 см
ВС = AD = 19 см

Хороший ответ

14 октября 2022 16:05

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Начертите неразвернутый угол AOB и проводите:1) луч OC, который делит угол AOB на две части; 2) луч OD, который не делит угол AOB на два угла.... В треугольнике MNP точка К лежит на отрезке MN, причем NKP – острый угол. Докажите, что KP < MP.... В остроугольном треугольнике ABC проведены высоты AA1 и BB1 . Докажите , что углы AA1B1 и ABB1 равны . С ЧЕРТЕЖОМ!!!... Сторона равностороннего треугольника равна 14√3.Найдите радиус окружности описанной около этого треугольника. СРОЧНО!!!... Как определить синус и косинус угла в 35 градусов.(Пожалуйста напишите решение если оно есть)...