Сформулируйте и докажите теорему о биссектрисе равнобедренного треугольника

1 ответ

Посмотреть ответы

m.pozharskiy

•Теорема. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
•Док-во.
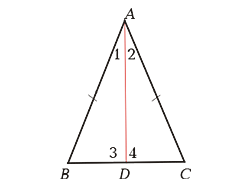
Обратимся к рисунку, на котором АВС — равнобедренный треугольник с основанием ВС, АD — его биссектриса.
Из равенства треугольников АВD и АСD (по 2 признаку равенства треугольников:AD-общая;углы 1 и 2 равны т.к. AD-биссектриса;AB=AC,т.к. треугольник равнобедренный) следует, что ВD = DC и 3 = 4. Равенство ВD = DC означает, что точка D — середина стороны ВС и поэтому АD — медиана треугольника АВС. Так как углы 3 и 4 смежные и равны друг другу, то они прямые. Следовательно, отрезок АО является также высотой треугольника АВС. Теорема доказана.

Хороший ответ

14 октября 2022 16:53

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Высота CD прямоугольного треугольника ABC отсекает от гипотенузы AB, равной 9 см, отрезок AD, равный 4 см. Докажите, что ∆ABC ~ ∆ACD и найдите AC.... На стороне CD квадрата ABCD лежит точка P так, что CP=PD, O-точка пересичений диогоналей. Выразите векторы BO, BP, PA через векторы x=BA и y=BC.... Один из углов равнобедренного треугольника равен 100 градусам. Найти другие углы.... Построить луч AD и отложить на нем отрезки АК и KD так, чтобы АК : KD = 2 : 5 (например, АК = 2 см, KD = 5 см). 2) Провести прямую BD. 3) Провести пря... Периметр ромба равен 40 см, а один из его углов равен 60 градусов. найдите площадь ромба,деленную на √3...