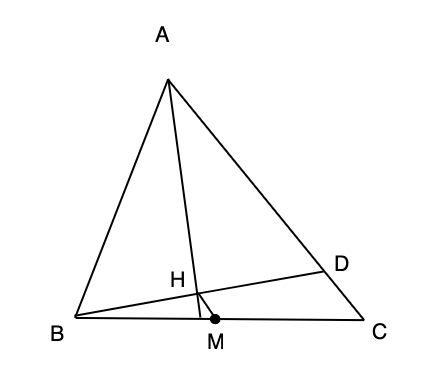
В треугольнике ABC известны длины сторон: AB=4, BC=5, CA=6. Точка M — середина отрезка BC, а точка H — основание перпендикуляра, опущенного из B на биссектрису угла A. Найдите длину отрезка HM. Если необходимо, ответ округлите до сотых.

1 ответ

Посмотреть ответы

Megamozg

2205

Точка D является пересечением BH со стороной AC. Треугольник ABD является равнобедренным,

АН - биссектриса и высота одновременно, то она явялется медианой стороны BD. Значит, H — середина отрезка BD.

Тогда HM — средняя линия треугольника BCD

Так как треугольник АВD равнобедренный, то сторона АD=АВ=4. Отсюда найдём CD:

СD=АС-AD=6-4=2

По свойству срединной линии мы знаем, что она параллельна третьей стороне и равняется её половине следовательно

НМ=DC/2=2/2=1

НМ=1

ЧТД

Хороший ответ

18 ноября 2022 08:58

Остались вопросы?

Найти нужный

Еще вопросы по категории Математика

В соответствии с национальным законодательством доход в размере до 500 тыс. руб. в год облагается налогом по ставке 12%; превышающий 500 тыс. руб., но... 1. Найдем уравнение прямой BC, проходящей через точки B(-5,2) и C(-2,3). Уравнение прямой через две точки можно найти, используя формулу: \[y - y_1... Масштаб карти 1:600 000.Визначте відстань на місцевості.якщо вона на карті зображена відрізком 3.см... помогите решить задачу с поля площадью 87 га сняли урожай 10450 ц а, с поля площадью113га собрали 14980 ц картофеля. найдите среднюю урожайность карто... Сколько слагаемых должно содержаться под корнем 3 над корнем √(5 в кубе+5 в кубе+…+5 в кубе) = 5 в кубе +5 в кубе, чтобы выполнялось равенство?...