Подскажите, пожалуйста, какой ответ?

Есть два готовых, но не могу понять, какой верный

Даны координаты вершин пирамиды ABCD

A (3,3,9) B(6,9,1) C(1,7,3) D(8,5,8)

Требуется найти:

1) длину ребра АВ

2) угол между ребрами АВ и AD

3) проекцию вектора AC на вектор AD

4) уравнение прямой AB

5) уравнение плоскости ABC

Сделать чертеж

Решение

1. Формула для вычисления расстояния между двумя

точками A(xa, ya, za) и B(xb, yb, zb) в пространстве:

AB=√ ( xb- xa )²+(yb- ya )²+(zb- za )²

Координаты точек заданы:

A (3,3,9) B(6,9,1) C(1,7,3) D(8,5,8)

Находим длину ребра АВ:

АВ=[(6-3)²+(9-3)²+(1-9)²]½=[3²+6²+(-8)²]½=[3²+6²+(-8)²]½=

=[9+36+64]½=109 ½=√109= 10,44

2. Угол между ребрами АВ и AD

Для нахождения углов треугольника по трём сторонам

используют теорему косинусов. Она гласит, что квадрат длины

любой стороны треугольника равен сумме квадратов длин двух

других сторон минус удвоенное произведение длин этих сторон на

косинус угла между ними.

Формула для расчёта углов с помощью теоремы косинусов:

cos(α) = (b² + e² - d²) / (2 × b × e) =

=(5,48²+10,44²-8,31²)/2 × 5,48 × 10,44 =

Вычислим квадраты чисел:

5,48²=5,48×5,48=30,03

10,44²=10,44×10,44=108,98

8,31²=8,31×8,31=69,03

Вычислим произведение в знаменателе:

2×5,48×10,44=2×57,1752=114,35

Выполним сложение и вычитание в числителе:

30,0304+108,9836−69,0361=70,98

Теперь поделим числитель на знаменатель:

70,98 / 114,35 ≈ 0,6207

Зная косинус угла α, по таблице Брадиса находим угол:

cos(α) = 0,6207, α=arccos (0.6207)=52°26´

Угол между ребрами АВ и AD α=52°26´

3. Найдем значение AE - проекции вектора AC на вектор AD

Для этого нужно знать третью сторону в треугольнике САD.

CD= √(8-1)²+(5-7)²+(8-3)²=8,83

т.е. CD=8,83, CE — это высота в треугольнике САD.

угол β находим по трем сторонам треугольника CAD (также

как находили угол α ), β = 84,4º

Проекция вектора AC на вектор AD

AE=AC×cos β =7,48 × cos 84,4º =7.48⋅0.109=0.81532

4. Уравнение прямой AB

Каноническое уравнение прямой имеет вид: (x - x₁) / (x₂ - x₁) = (y -

y₁) / (y₂ - y₁) =(z - z₁) / (z₂- z₁)

Подставим

(x-3)/3= (y-3)/6=(z-9)/-8

или

8x-24=4y-12=27-3z

уравнение прямой AB

8x-4y+3z-39=0

Проверка

8×3-4×3+3×9-39=24-12+27-39=39-39=0

5. Уравнение плоскости, проходящей через три произвольные

точки А, В, С, имеет вид:

Кx +Ly+Mz+1=0,

где K,L,M – коэффициенты, которые требуется найти.

Подставим координаты каждой точки в это уравнение, получим

систему из трех уравнений {координаты заданы A (3,3,9) B(6,9,1)

C(1,7,3) D(8,5,8)}

3×K+3×L+9×M+1=0

6×K+9×L+M+1=0

K+7×L+3×M+1=0

K=2/153

L=-1/9

M=-4/51

Тогда уравнение примет вид

2x/153-y/9-4z/51+1=0

или

2x-17y-12z=-153

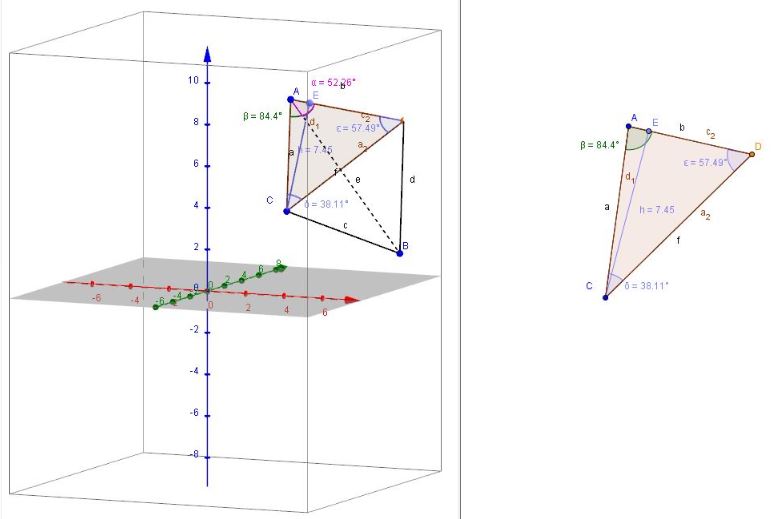
Чертеж представлен.

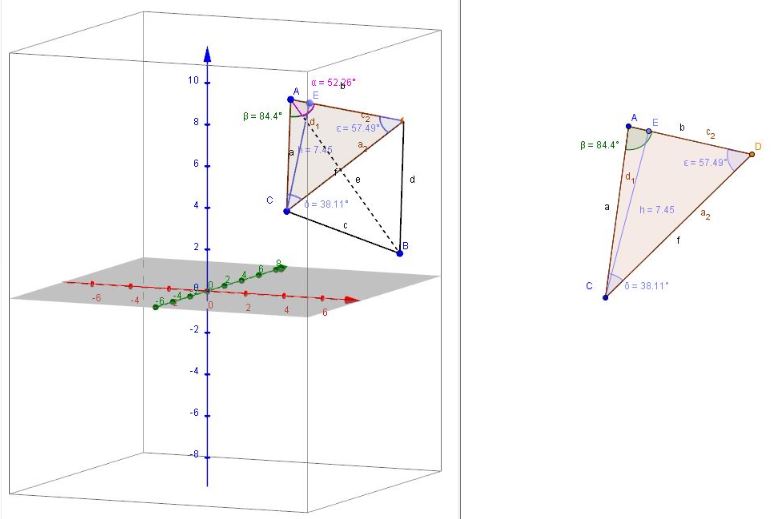
Даны координаты вершин пирамиды ABCD

A (3,3,9) B(6,9,1) C(1,7,3) D(8,5,8)

Требуется найти:

1) длину ребра АВ

2) угол между ребрами АВ и AD

3) проекцию вектора AC на вектор AD

4) уравнение прямой AB

5) уравнение плоскости ABC

Сделать чертеж

Решение

1. Формула для вычисления расстояния между двумя точками A(x_a, y_a, z_a) и B(x_b, y_b, z_b) в пространстве:

1. AB=√ ( x_b- x_a )²+(y_b- y_a )²+(z_b- z_a )²

Координаты точек заданы:

A (3,3,9) B(6,9,1) C(1,7,3) D(8,5,8)

Находим длину ребра АВ:

АВ=[(6-3)²+(9-3)²+(1-9)²]½=[3²+6²+(-8)²]½=[3²+6²+(-8)²]½=

=[9+36+64]½=109 ½=√109= 10,44

2. Угол между ребрами АВ и AD

Для нахождения углов треугольника по трём сторонам используют теорему косинусов. Она гласит, что квадрат длины любой стороны треугольника равен сумме квадратов длин двух других сторон минус удвоенное произведение длин этих сторон на косинус угла между ними.

Формула для расчёта углов с помощью теоремы косинусов:

cos(α) = (b² + e² - d²) / (2 × b × e) =

=(5,48²+10,44²-8,31²)/2 × 5,48 × 10,44 =

Вычислим квадраты чисел:

5,48²=5,48×5,48=30,03

10,44²=10,44×10,44=108,98

8,31²=8,31×8,31=69,03

Вычислим произведение в знаменателе:

2×5,48×10,44=2×57,1752=114,35

Выполним сложение и вычитание в числителе:

30,03+108,98−69,03=70,98

Теперь поделим числитель на знаменатель:

70,98 / 114,35 ​≈ 0,6207

Зная косинус угла α, по таблице Брадиса находим угол:

cos(α) = 0,6207, α=arccos (0.6207)=52°26´

Угол между ребрами АВ и AD α=52°26´

3. Найдем значение AE - проекции вектора AC на вектор AD

Для этого нужно знать третью сторону в треугольнике САD.

CD= √(8-1)²+(5-7)²+(8-3)²=8,83

т.е., CD=8,83, CE — это высота в треугольнике САD.

угол β находим по трем сторонам треугольника CAD (также как находили угол α ), β = 84,4º

Проекция вектора AC на вектор AD

AE=AC×cos β =7,48 ×cos 84,4º =7.48⋅0.109=0.81532

4. Уравнение прямой AB

Каноническое уравнение прямой имеет вид: (x - x₁) / (x₂ - x₁) = (y - y₁) / (y₂ - y₁) =(z - z₁) / (z₂- z₁)

Подставим

(x-3)/3= (y-3)/6=(z-9)/-8

или

8x-24=4y-12=27-3z

уравнение прямой AB

8x-4y+3z-39=0

Проверка

8×3-4×3+3×9-39=24-12+27-39=39-39=0

5. Уравнение плоскости, проходящей через три произвольные точки А, В, С, имеет вид:

Кx +Ly+Mz+1=0,

где K,L,M – коэффициенты, которые требуется найти.

Подставим координаты каждой точки в это уравнение, получим систему из трех уравнений {координаты заданы A (3,3,9) B(6,9,1) C(1,7,3) D(8,5,8)}

3×K+3×L+9×M+1=0

6×K+9×L+M+1=0

K+7×L+3×M+1=0

K=2/153

L=-1/9

M=-4/51

Тогда уравнение примет вид

2x/153-y/9-4z/51+1=0

или

2x-17y-12z=-153

Чертеж представлен на фото.