1 Точка касания двух окружностей равноудалёна от центров этих окружностей.2 В параллелограмме есть два равных угла .
3 Площадь прямоугольного треугольника равна произведению длин его катетов.
Какое из следующих утверждений верно ?

2 ответа

Посмотреть ответы

y.visockiy

Ответ:

2).

Объяснение:

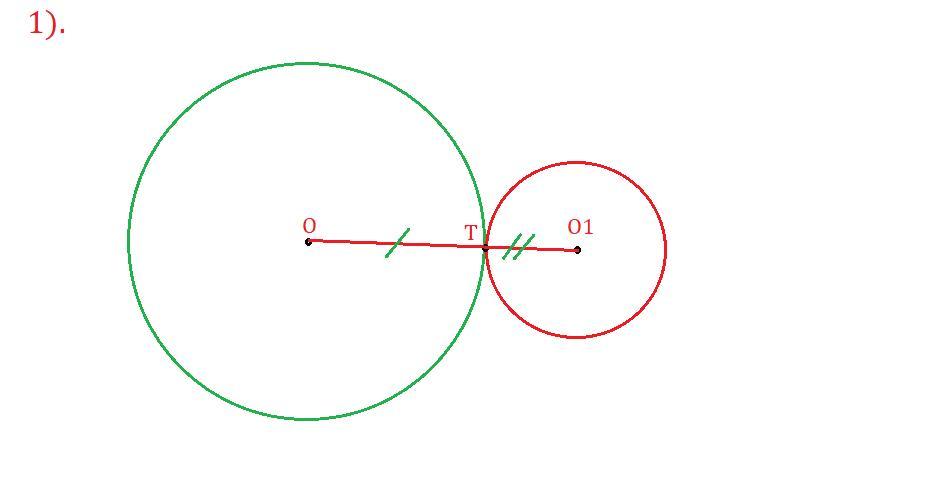
1) Неверно, так как окружности могут быть совершенно разных радиусов.
Например, рассмотрим рисунок "1)".
На рисунке изображены две окружности с центром в точке $O$ и с центром в точке $O1$ . Их точка касания - точка $T$ . Заметим, что $OT > O1T$ , поэтому точка $T$ не равноудалена от точек $O$ и $O_1$ .
2) Верно.
Свойство: "У параллелограмма противоположные углы равны".
В параллелограмме всего 4 угла, поэтому в нём есть по 2 равных угла. (рисунок 2).
3) Неверно.
Площадь прямоугольного треугольника равна полупроизведению его катетов.
Т.е. $S$ прямоугольного треугольника = (катет · второй катет) : 2.

Хороший ответ

2 декабря 2022 01:38

d.scherbetov

1. Точка касания двух окружностей равноудалена от центров этих окружностей.

Неверно. Точка окружности находится от её центра на расстоянии равным радиусу этой окружности, поэтому утверждение верно только для двух равных окружностей.

2. В параллелограмме есть два равных угла.

Верно. В параллелограмме противоположные углы равны, поэтому есть две пары равных углов.

3. Площадь прямоугольного треугольника равна произведению длин его катетов.

Неверно. Площадь прямоугольного треугольника равна полупроизведению длин его катетов.
Ответ: 2.

2 декабря 2022 01:38

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Треугольник ABC , AD:DB = AE:EC, BC=25. DE=?... Дана восьмиугольная пирамида. Сколько у нее граней?... Какие из следующих утверждений верны? 1) Вписанные углы окружности равны. 2) Через любые 3точки, не принадлежащие одной прямой, проходит единственная... Найдите площадь четырехугольника, изображенного на рисунке, если стороны клеток равны 1 см.... Про невырожденный треугольник ABC известно, что AB=3.5, AC=2.4, а длина стороны BC выражается целым числом n. Чему может быть равно n? Если ответов не...