В конус вписана пирамида. основанием пирамиды служит прямоугольный треугольник, катет которого равен 2а, а прилежащий угол равен 30°. боковая грань пирамиды,проходящая через данный катет,составляет с плоскостью основания угол 45°. найдите объем конуса.

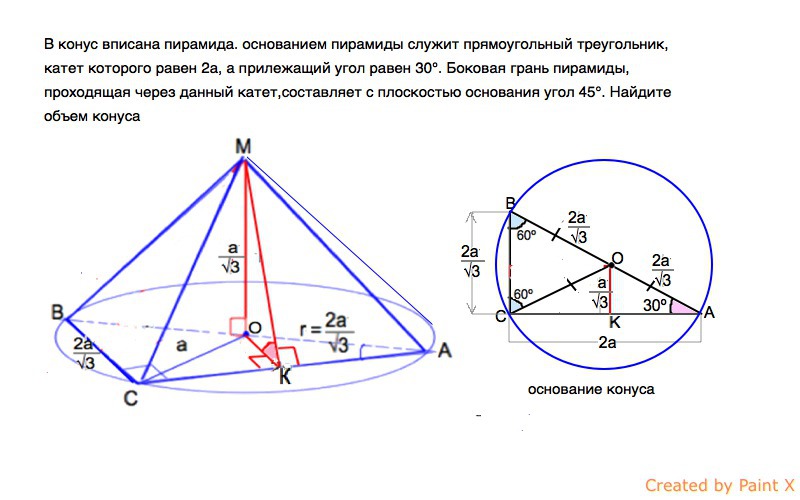
В конус вписана пирамида. основанием пирамиды служит прямоугольный треугольник, катет которого равен 2а, а прилежащий угол равен 30°. Боковая грань пирамиды,проходящая через данный катет,составляет с плоскостью основания угол 45°. Найдите объем конуса.
V=S•H:3
Для ответа на вопрос задачи нужно найти радиус основания конуса и его высоту ( она равна высоте вписанной пирамиды).
Основание пирамиды - прямоугольный треугольник. Следовательно, радиус основания конуса, как описанной окружности, равен половине гипотенузы вписанного треугольника.
Пусть это ∆ АВС, ∠С=90º, ∠А=30º; АС=2а
Гипотенуза АВ=АС:cos 30º=4a/√3
Тогда R=АО=ВО=ОС=2a/√3
Катет ВС=2a/√3 как противолежащий углу 30º
Угол между боковой гранью и плоскостью основания равен углу между перпендикулярами, проведенными к О и М из точки К катета АС (МК - наклонная, ОК - ее проекция, МК и ОК перпендикулярны АС по т. о трех перпендикулярах). К - середина основания АС равнобедренного ∆ АОС
Т.к. угол ОКА=90º, ОК|| ВС и является средней линией ∆ АВС и равна половине ВС.
ОК=ВС:2=а/√3
Высота пирамиды МО перпендикулярна плоскости основания, угол МКО=45º по условию, и ∆ МОК - равнобедренный. МО=ОК=а/√3
S осн. конуса=πR²=4π•a²/3
V=[(4π•а²/3)•a/√3]:3=4π•a³/√3 (ед. объема)