Помогите решить:А) sinx(2sinx -3ctgx)=3
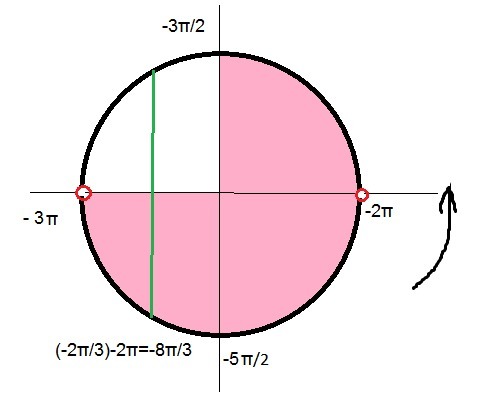
Б) Найдите все корни уравнения на промежутке [-3Пи, -3Пи/2]

ОДЗ: sinx≠0 ⇒ x≠πk, k∈Z.

Умножаем на sinx≠0
sinx·(2sin²x-3cosx)=3sinx;
sinx·(2sin²x-3cosx)-3sinx=0;
sinx·(2-2cos²x-3cosx-3)=0;
sinx·(2cos²x+3cosx+1)=0
sinx≠0
2cos²x+3cosx+1=0
D=9-2·4=1
cosx=-1 или cosx=-1/2
x=π+2πn, n∈Z или х=± (2π/3)+2πk, k∈Z
не удовл. ОДЗ

б)
х=-(2π/3)-2π=-8π/3∈[-3π, -3π/2]

О т в е т. а) ± (2π/3)+2πk, k∈Z б) -8π/3∈[-3π, -3π/2]